
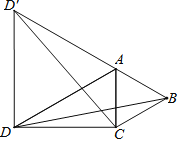
【题目】如图,在△ACD中,AD=9,CD=![]() ,△ABC中,AB=AC,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
,△ABC中,AB=AC,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
(1)求证:BD=CD′
(2)求BD的长.
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
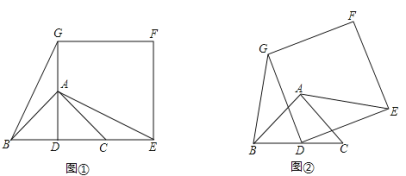
【题目】如图(1),已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的关系(位置关系及数量关系),请直接写出你得到的结论;
(2)将正方形DEFG绕点D逆时针方向旋转一角度α后(0°<α<90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;
(3)若BC=DE=2,正方形DEFG绕点D逆时针方向旋转角度α (0°<α<360°)过程中,当BG为最小值时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
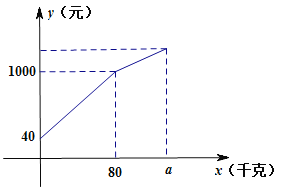
【题目】一果农带了若干千克自产的苹果进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又半价售完剩下的苹果.售出苹果千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)果农自带的零钱是多少?
(2)降价前他每千克苹果出售的价格是多少?
(3)降价售完剩余苹果后,这时他手中的钱(含备用零钱)是1120元,问果农一共带了多少千克苹果?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅计划购买12张餐桌和一批椅子(不少于12把),现从甲、乙两商场了解到同一型号的餐桌报价都为每张200元,餐椅报价都为每把50元.甲商场规定:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌、餐椅均按报价的八五折销售,那么,什么情况下到甲商场购买更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
在平面直角坐标系中,二元一次方程x-y=0的一个解![]() 可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
直线x-y=0把坐标平面分成直线上方区域,直线上,直线下方区域三部分,如果点M(x0,y0)的坐标满足不等式x-y≤0,那么点M(x0,y0)就在直线x-y=0的上方区域内。特别地,x=k(k为常数)表示横坐标为k的点的全体组成的一条直线,y=m(m为常数)表示纵坐标为m的点的全体组成的一条直线。
请根据以上材料,探索完成以下问题:
(1)已知点A(2,1)、B(![]() ,
,![]() )、C(
)、C(![]() ,
,![]() )、D(4,
)、D(4,![]() ),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
(2)已知点P(x,y)的坐标满足不等式组![]() ,则所有的点P组成的图形的面积是 ;
,则所有的点P组成的图形的面积是 ;
(3)已知点P(x,y)的坐标满足不等式组 ,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点。
(1)画出![]() 向下平移2个单位,再向右平移3个单位后得到的
向下平移2个单位,再向右平移3个单位后得到的![]() ;
;
(2)图中![]() 与
与![]() 的关系是:____________________;
的关系是:____________________;
(3)图中![]() 的面积是___________________________。
的面积是___________________________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com