
����Ŀ������������y= ![]() ��x��0����ͼ���߶�OA�Ķ˵�A��OΪԭ�㣬��AB��x���ڵ�B����B������Ϊ��2��0����tan��AOB=
��x��0����ͼ���߶�OA�Ķ˵�A��OΪԭ�㣬��AB��x���ڵ�B����B������Ϊ��2��0����tan��AOB= ![]() �����߶�AB��x��������ƽ�Ƶ��߶�DC��λ�ã�����������y=
�����߶�AB��x��������ƽ�Ƶ��߶�DC��λ�ã�����������y= ![]() ��x��0����ͼ��ǡ�þ���DC���е�E��
��x��0����ͼ��ǡ�þ���DC���е�E��
��1����k��ֵ��ֱ��AE�ĺ�������ʽ��
��2����ֱ��AE��x�ύ�ڵ�M����y�ύ�ڵ�N������̽���߶�AN���߶�ME�Ĵ�С��ϵ��д����Ľ��۲�˵�����ɣ�
���𰸡�
��1��
�⣺����֪�ã���Rt��OAB�У�OB=2��tan��AOB= ![]() ��
��
��AB=3��
��A���������2��3����
��k=xy=6��
��DC��ABƽ�Ƶõ�����EΪDC���е㣬
���E��������Ϊ ![]() ��
��
�֡ߵ�E��y= ![]() ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
���E��������4�� ![]() ����
����
��ֱ��MN�ĺ�������ʽΪy=k1x+b��
�� 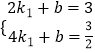 ��
��
��� 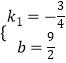 ��
��
��ֱ��MN�ĺ�������ʽΪy=�� ![]() x+
x+ ![]()
��2��
�⣺���ۣ�AN=ME��
���ɣ��ڱ���ʽy=�� ![]() x+
x+ ![]() �У�
�У�
��y=0�ɵ�x=6����x=0�ɵ�y= ![]() ��
��
���M��6��0����N��0�� ![]() ����
����
�ӳ�DA��y���ڵ�F��
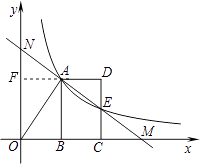
��AF��ON����AF=2��OF=3��
��NF=ON��OF=x����CM=6��4=2=AF��EC= ![]() =NF��
=NF��
�ڡ�ANF���MEC�У� 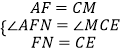 ��
��
���ANF�ա�MEC��
��AN=ME��
����������1������֪�ã���Rt��OAB�У�OB=2��tan��AOB= ![]() �����AB=3������y=
�����AB=3������y= ![]() �õ�k=xy=6��������֪�����õ���E��������Ϊ
�õ�k=xy=6��������֪�����õ���E��������Ϊ ![]() ���ɵ�E��˫����y=
���ɵ�E��˫����y= ![]() ��x��0����ͼ���ϣ��õ���E������Ϊ��4��
��x��0����ͼ���ϣ��õ���E������Ϊ��4�� ![]() �����ⷽ���鼴�ɵõ����ۣ���2������y=��
�����ⷽ���鼴�ɵõ����ۣ���2������y=�� ![]() x+
x+ ![]() ��õ�M��6��0����N��0��
��õ�M��6��0����N��0�� ![]() �����ӳ�DA��y���ڵ�F����AF��ON����AF=2��OF=3������ȫ�������ε����ʼ��ɵõ����ۣ�
�����ӳ�DA��y���ڵ�F����AF��ON����AF=2��OF=3������ȫ�������ε����ʼ��ɵõ����ۣ�
�����㾫����ͨ��������÷�����������ͼ��ͷ��������������ʣ����շ�����������ͼ������˫���ߣ�������������ͼ�������Գ�ͼ���������ĶԳ�ͼ�Σ��������Գ��ֱ��y=x�� y=-x���Գ������ǣ�ԭ�㣻����:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ������������Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x��1�뷴��������y= ![]() ��ͼ����A��B���㣬��x�ύ�ڵ�C����֪��A������Ϊ����1��m����
��ͼ����A��B���㣬��x�ύ�ڵ�C����֪��A������Ϊ����1��m���� 
��1�����������Ľ���ʽ��
��2������P��n����1���Ƿ���������ͼ����һ�㣬����P��PE��x���ڵ�E���ӳ�EP��ֱ��AB�ڵ�F�����CEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�DZ߳�Ϊ4�ĵȱ������Σ���O�ڱ�AB�ϣ���O����B�ҷֱ����AB��BC�ཻ�ڵ�D��E��EF��AC������ΪF�� 
��1����֤��ֱ��EF�ǡ�O�����ߣ�
��2����ֱ��DF���O����ʱ�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=x2+bx+c��y=x��ͼ����ͼ��ʾ�������½��ۣ�
��b2��4c��0��
��b+c+1=0��
��3b+c+6=0��
�ܵ�1��x��3ʱ��x2+��b��1��x+c��0��
������ȷ�ĸ���Ϊ�� ��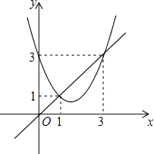
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬����ABC��ֱ��MN���ۺ���Cǡ������AB���ϵĵ�D������֪MN��AB��MC=6��NC= ![]() �����ı���MABN������ǣ� ��
�����ı���MABN������ǣ� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����Ӧ�ã�������������⣺
��1����ͼ�٣���֪����Rt��ABC�У���C=90�㣬��OΪAB���е㣬����POQ=90�㣬�ֱ�AC��BC�ڵ�P��Q������PQ��CO����֤��AP2+BQ2=PQ2�� 
��2����ͼ�ڣ�������Rt��ABC��Ϊ����ֱ�������Σ���O��ΪAB���е㣬��POQ=90�㣬��̽����������AP2+BQ2=PQ2�Ƿ��Գ����� 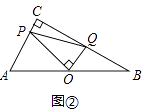
��3��ͨ������̽������ֱ�������������ۣ����Խ����������⣺��ͼ�ۣ���֪Rt��ABC�У���C=90�㣬AC=6��BC=8����OΪAB���е㣬��C��O�����Բ�ֱ�AC��BC��P��Q������PQ�����PCQ��������ֵ�� 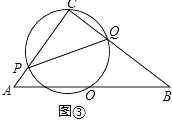
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������A��B����������9����ͬʱ������������У���֪���ٶȱ��ҿ�2ǧ��/ʱ��������11ʱ���������36ǧ�ף��ֹ���2Сʱ�����������36ǧ��.
��1����������ؼ�ľ������������ٶȣ�
��2�������������ֱ��A��B����ͬʱ������У���B��A���غ��������أ���������һ�������͵ڶ����������ߵ�ʱ���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���Ѿ���OCBA������ֱ������ϵ�У�OC=3��BC=2��ȡAB���е�M������MC���ѡ�MBC��x��ĸ�����ƽ��OC�ij��Ⱥ�õ���DAO��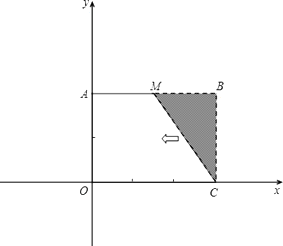
��1����ֱ��д����D�����ꣻ
��2����֪��B���D�ھ���ԭ����������ϣ���P�ڵ�һ�����ڵĸ����������ƶ�������P��PQ��x���ڵ�Q������OP��
������O��P��QΪ��������������DAO���ƣ��������P�����ꣻ
�������������ߵĶԳ������Ƿ����һ��T��ʹ��|TO��TB|��ֵ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com