
����Ŀ����֪����ͼ���Ѿ���OCBA������ֱ������ϵ�У�OC=3��BC=2��ȡAB���е�M������MC���ѡ�MBC��x��ĸ�����ƽ��OC�ij��Ⱥ�õ���DAO��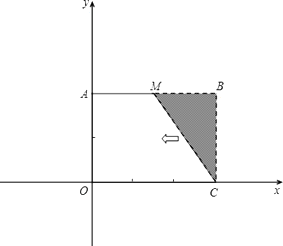
��1����ֱ��д����D�����ꣻ
��2����֪��B���D�ھ���ԭ����������ϣ���P�ڵ�һ�����ڵĸ����������ƶ�������P��PQ��x���ڵ�Q������OP��
������O��P��QΪ��������������DAO���ƣ��������P�����ꣻ
�������������ߵĶԳ������Ƿ����һ��T��ʹ��|TO��TB|��ֵ���
���𰸡�
��1��
�⣺������ã�D���� ![]() ��2����
��2����
��2��
�⣺�١�OC=3��BC=2��
��B��3��2����
�������߾���ԭ�㣬
���������ߵĽ���ʽΪy=ax2+bx ��a��0��
�������߾�����B��3��2�����D���� ![]() ��2����
��2����
�� 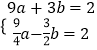
��ã� 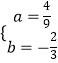
�������ߵĽ���ʽΪy= ![]() ��
��
�ߵ�P���������ϣ�
�����P��x�� ![]() ����
����
1��������PQO�ס�DAO���� ![]() ��
��  ��
��
��ã�x1=0����ȥ����x2= ![]() ��
��
���P�� ![]() ����
����
2��������OQP�ס�DAO���� ![]() ��
�� 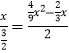 ��
��
��ã�x1=0����ȥ����x2= ![]() ��
��
���P�� ![]() ��6����
��6����
�ڴ��ڵ�T��ʹ��|TO��TB|��ֵ���
������y= ![]() �ĶԳ���Ϊֱ��x=
�ĶԳ���Ϊֱ��x= ![]() ������������x�����һ������ΪE�����E��
������������x�����һ������ΪE�����E�� ![]() ��0����
��0����
�ߵ�O����E����ֱ��x= ![]() �Գƣ�
�Գƣ�
��TO=TE
Ҫʹ��|TO��TB|��ֵ���
����ʹ��|TE��TB|��ֵ���
��������������֮��С�ڵ����߿�֪����T��E��B������ͬһֱ����ʱ��|TE��TB|��ֵ���
���B��E�����ֱ�߽���ʽΪy=kx+b��k��0����
�� 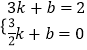
��ã� 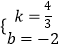
��ֱ��BE�Ľ���ʽΪy= ![]() x��2��
x��2��
��x= ![]() ʱ��y=
ʱ��y= ![]()
�����һ��T�� ![]() ����1��ʹ��|TO��TB|���
����1��ʹ��|TO��TB|���
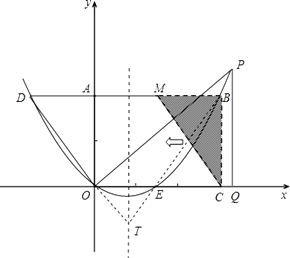
����������1������M��AB���е㣬���ɵõ�AM= ![]() ���ɴ˿����M������꣬��M����������ƽ��3����λ���ɵõ���D�����ꣻ��2���ٸ���B��D�����꼴��ȷ�������ߵĽ���ʽ�����P��ĺ����꣬���������ߵĽ���ʽ�ɵõ�P��������ı���ʽ�����ڡ�PQO=��DAO=90�㣬����O��P��QΪ��������������DAO���ƣ��������������1������PQO�ס�DOA��2������OQP�ס�DAO��������������������õIJ�ͬ�����߶Σ��������P������ꣻ������D��B���������ߵĶԳ���Գƣ���|TO��TB|��ֵ�����ôT���Ϊֱ��DO�������߶Գ���Ľ��㣬���������ߵĽ���ʽ�������Գ��᷽�̣�����D�����������ֱ��DO�Ľ���ʽ���������������Ľ���ʽ���������T������꣮
���ɴ˿����M������꣬��M����������ƽ��3����λ���ɵõ���D�����ꣻ��2���ٸ���B��D�����꼴��ȷ�������ߵĽ���ʽ�����P��ĺ����꣬���������ߵĽ���ʽ�ɵõ�P��������ı���ʽ�����ڡ�PQO=��DAO=90�㣬����O��P��QΪ��������������DAO���ƣ��������������1������PQO�ס�DOA��2������OQP�ס�DAO��������������������õIJ�ͬ�����߶Σ��������P������ꣻ������D��B���������ߵĶԳ���Գƣ���|TO��TB|��ֵ�����ôT���Ϊֱ��DO�������߶Գ���Ľ��㣬���������ߵĽ���ʽ�������Գ��᷽�̣�����D�����������ֱ��DO�Ľ���ʽ���������������Ľ���ʽ���������T������꣮
�����㾫����������Ŀ����֪���������ö��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABΪֱ����O��BC�ڵ�D������D��EF��AC�ڵ�E����AB���ӳ����ڵ�F�� 
��1���ж�ֱ��DE���O��λ�ù�ϵ����˵�����ɣ�
��2�����AB=5��BC=6����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y= ![]() ��x��0����ͼ���߶�OA�Ķ˵�A��OΪԭ�㣬��AB��x���ڵ�B����B������Ϊ��2��0����tan��AOB=
��x��0����ͼ���߶�OA�Ķ˵�A��OΪԭ�㣬��AB��x���ڵ�B����B������Ϊ��2��0����tan��AOB= ![]() �����߶�AB��x��������ƽ�Ƶ��߶�DC��λ�ã�����������y=
�����߶�AB��x��������ƽ�Ƶ��߶�DC��λ�ã�����������y= ![]() ��x��0����ͼ��ǡ�þ���DC���е�E��
��x��0����ͼ��ǡ�þ���DC���е�E��
��1����k��ֵ��ֱ��AE�ĺ�������ʽ��
��2����ֱ��AE��x�ύ�ڵ�M����y�ύ�ڵ�N������̽���߶�AN���߶�ME�Ĵ�С��ϵ��д����Ľ��۲�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���ACB=90�㣬��B=60�㣬DΪAB���е㣬��EDF=90�㣬DE��AC�ڵ�G��DF������C��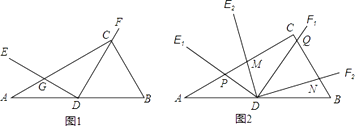
��1�����ADE�Ķ�����
��2����ͼ2����ͼ1�еġ�EDF�Ƶ�D˳ʱ�뷽����ת�Ǧ���0�㣼����60�㣩����ת�����е���������λ�÷ֱ��Ϊ��E1DF1 �� ��E2DF2 �� DE1��ֱ��AC�ڵ�P��DF1��ֱ��BC�ڵ�Q��DE2��ֱ��AC�ڵ�M��DF2��ֱ��BC�ڵ�N���� ![]() ��ֵ��
��ֵ��
��3����ͼ1�С�B=�£�60�㣼�£�90�㣩����2���е������������䣬�ж� ![]() ��ֵ�Ƿ�Ϊ��ֵ������ǣ���ֱ��д�����ֵ���ú��µ�ʽ�ӱ�ʾ����������ǣ���˵�����ɣ�
��ֵ�Ƿ�Ϊ��ֵ������ǣ���ֱ��д�����ֵ���ú��µ�ʽ�ӱ�ʾ����������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���AOB=60�㣬��B����Ϊ��2��0�����߶�OA�ij�Ϊ6������AOB�Ƶ�O��ʱ����ת60���A���ڵ�C������B���ڵ�D����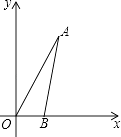
��1������ͼ�л�����COD��
��2�����A��ת��������������·�̣���ȷ��0.1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ַ����ս��𣬾�������������±���ʾ�������ж��������ݵ�˵���в���ȷ���ǣ� ��
�� �� | 1 | 3 | 5 | 70 | 10 | 8 | 3 |
��Ԫ�� | 200000 | 150000 | 80000 | 15000 | 10000 | 8000 | 5000 |
A.������195000
B.�����15000
C.������15000
D.ƽ������15000
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С����5��д�Ų�ͬ���ֵĿ�Ƭ�����㰴Ҫ������Ƭ������������⣺
![]()
��1������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ�����ֵij˻���˻������ֵ���� ����
��2������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������������С�����̵���Сֵ���� ����
��3������ȡ��4�ſ�Ƭ����ѧ���ļ��㷽����ʹ������Ϊ24����д���������ʽ��������д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0��ͼ��Ķ���ΪD����ͼ����x��Ľ���A��B�ĺ�����ֱ�Ϊ��1��3�������н�����ȷ���ǣ������� 
A.2a��b=0
B.a+b+c��0
C.3a��c=0
D.��a= ![]() ʱ����ABD�ǵ���ֱ��������
ʱ����ABD�ǵ���ֱ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com