
【题目】如图,过原点的直线与反比例函数![]() (k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.
(k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.

【答案】6
【解析】
连接O,CE,过点A作AF⊥x轴,过点D作DH⊥x轴,过点D作DG⊥AF;由AB经过原点,则A与B关于原点对称,再由BE⊥AE,AE为∠BAC的平分线,
可得AD∥OE,进而可得S△ACE=S△AOC;设点A![]() ,由已知条件AC=3DC,DH∥AF,可得3DH=AF,则点D
,由已知条件AC=3DC,DH∥AF,可得3DH=AF,则点D![]() ,证明△DHC∽△AGD,得到S△HDC=
,证明△DHC∽△AGD,得到S△HDC=![]() S△ADG, 所以S△AOC=S△AOF+S梯形AFHD+S△HDC=
S△ADG, 所以S△AOC=S△AOF+S梯形AFHD+S△HDC=![]() ,即可求解.
,即可求解.
连接OE,CE,过点A作AF⊥x轴,过点D作DH⊥x轴,过点D作DG⊥AF,

∵过原点的直线与反比例函数![]() (k>0)的图象交于A,B两点,
(k>0)的图象交于A,B两点,
∴A与B关于原点对称,
∴O是AB的中点,
∵BE⊥AE,
∴OE=OA,
∴∠OAE=∠AEO,
∵AE为∠BAC的平分线,
∴∠DAE=∠AEO,
∴AD∥OE,
∴S△ACE=S△AOC,
∵AC=3DC,△ADE的面积为8,
∴S△ACE=S△AOC=12,
设点A![]() ,
,
∵AC=3DC,DH∥AF,得3DH=AF,
∴D![]()
∵CH∥GD,AG∥DH
∴△DHC∽△AGD,
∴S△HDC=![]() S△ADG,
S△ADG,
∴S△AOC=S△AOF+S梯形AFHD+S△HDC=![]() ,
,
∴2k=12,k=6
故答案为:6.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市发现一种新型冠状病毒感染引起的急性呼吸道传染病.感染者的临床表现为:以发热、乏力、干咳为主要表现.约半数患者多在一周后出现呼吸困难,严重者快速进展为急性呼吸窘迫综合征、脓毒症休克、难以纠正的代谢性酸中毒和出凝血功能障碍.国家卫健委已发布1号公告,将新型冠状病毒感染的肺炎纳入传染病防治法规定的乙类传染病,但采取甲类传染病的预防、控制措施,同时将其纳入检疫传染病管理.
(1)在“新冠”初期,有2人感染了“新冠”,经过两轮传染后共有288人感染了“新冠”(这两轮感染均未被发现未被隔离),则每轮传染中平均一个人传染了几个人?
(2)某小区物管为预防业主感染传播购买![]() 型和
型和![]() 型两种
型两种![]() 口罩,购买
口罩,购买![]() 型
型![]() 口罩花费了2500元,购买
口罩花费了2500元,购买![]() 型
型![]() 口罩花费了2000元,且购买
口罩花费了2000元,且购买![]() 型
型![]() 口罩数量是购买
口罩数量是购买![]() 型
型![]() 口罩数量的2倍,已知购买一个
口罩数量的2倍,已知购买一个![]() 型
型![]() 口罩比购买一个
口罩比购买一个![]() 型
型![]() 口罩多花3元则该物业购买
口罩多花3元则该物业购买![]() 、
、![]() 两种
两种![]() 口罩的单价为多少元?
口罩的单价为多少元?
(3)由于实际需要,该物业决定再次购买这两种![]() 口罩,已知此次购进
口罩,已知此次购进![]() 型和
型和![]() 型两种
型两种![]() 口罩的数量一共为1000个,恰逢市场对这两种
口罩的数量一共为1000个,恰逢市场对这两种![]() 口罩的售价进行调整,
口罩的售价进行调整,![]() 型
型![]() 口罩售价比第一次购买时提高了
口罩售价比第一次购买时提高了![]() ,
,![]() 型
型![]() 口罩按第一次购买时售价的1.5倍出售,如果此次购买
口罩按第一次购买时售价的1.5倍出售,如果此次购买![]() 型和
型和![]() 型这两种
型这两种![]() 口罩的总费用不超过7800元,那么此次最多可购买多少个
口罩的总费用不超过7800元,那么此次最多可购买多少个![]() 型
型![]() 口罩?
口罩?
查看答案和解析>>
科目:初中数学 来源: 题型:
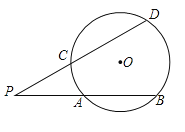
【题目】我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
(1)判断:图中有没有圆外角?如果有,请用字母表示出来.
(2)运用所学的数学知识,探究:圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系?将你的发现,用文字表述出来,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F
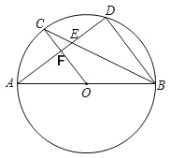
(1)求证:![]() =
=![]() ;
;![]()
(2)若CE=1,EB=3,求⊙O的半径;
(3)若BD=6,AB=10,求D E的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.
(1)求购进 A、B 两种树苗的单价;
(2)若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用60天的时间销售一种成本为10元每件的商品,经过统计得到此商品的日销售量m(件)、销售单价n(元/件)在第x天(x为正整数)销售的相关信息:
①m与x满足一次函数关系,且第1天的日销售量为98件,第4天的日销售量为92件;
②n与x的函数关系式为:n=![]() .
.
(1)求出第15天的日销售量;
(2)设销售该产品每天利润为y元,请写出y与x的函数关系式,并求出在60天内该产品的最大利润.
(3)在该产品的销售过程中,共有 天销售利润不低于2322元.(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨![]() 元(
元(![]() 为非负整数),每个月的销售利润为
为非负整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价定为多少元时,每个月的利润恰好是1920元?这时每件商品的利润率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论:①2a>b;②a﹣b+c>0;③a<b;④a>c,其中正确的结论是( )
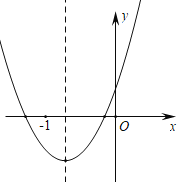
A.①③B.②③C.①④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
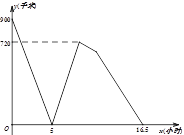
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达
两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达![]() 地后马上以另一速度原路返回
地后马上以另一速度原路返回![]() 地(掉头的时间忽略不计),乙车到达
地(掉头的时间忽略不计),乙车到达![]() 地以后即停在
地以后即停在![]() 地等待甲车.如图所示为甲乙两车间的距离
地等待甲车.如图所示为甲乙两车间的距离![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (小时)之间的函数图象,则当乙车到达
(小时)之间的函数图象,则当乙车到达![]() 地的时候,甲车与
地的时候,甲车与![]() 地的距离为__________千米.
地的距离为__________千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com