
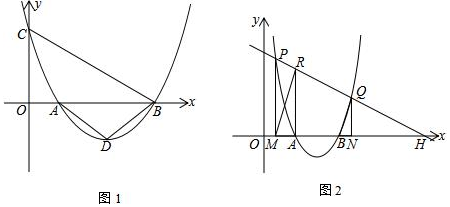
 如图,已知直线EF交x轴于点E(18,0),交y轴于点F,∠FEO=30°,C、D为EF上两点,且两点的横坐标分别为12和6;DA⊥y轴于点A,CB⊥y轴于点B,CQ⊥x轴于点Q.
如图,已知直线EF交x轴于点E(18,0),交y轴于点F,∠FEO=30°,C、D为EF上两点,且两点的横坐标分别为12和6;DA⊥y轴于点A,CB⊥y轴于点B,CQ⊥x轴于点Q.分析 (1)首先求出点F的坐标,利用待定系数法即可解决问题;
(2)作点Q关于直线CD的对称点Q′,易知Q′(15,3$\sqrt{3}$),连接OQ′交CD于P,此时△OPQ的周长最小.求出直线OQ′的解析式,利用方程组求出解得P的坐标即可解决问题;
(3)观察图象可知,只有点M在BC上时,存在OM=MN,如图:作MH⊥ON于H.构建方程即可解决问题;
解答 解:(1)在Rt△EOF中,∵OE=18,∠OEF=30°,
∴OF=OE•tan30°=6$\sqrt{3}$,
∴F(0,6$\sqrt{3}$),
设直线EF的解析式为y=kx+b,则有$\left\{\begin{array}{l}{18k+b=0}\\{b=6\sqrt{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=6\sqrt{3}}\end{array}\right.$,
∴$y=-\frac{{\sqrt{3}}}{3}x+6\sqrt{3}$;
∵D(6,4$\sqrt{3}$),C(12,2$\sqrt{3}$),
∴$A({0,4\sqrt{3}}),B({0,2\sqrt{3}})$.
(2)作点Q关于直线CD的对称点Q′,易知Q′(15,3$\sqrt{3}$),连接OQ′交CD于P,此时△OPQ的周长最小.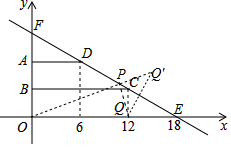
∵直线OQ′的解析式为y=$\frac{\sqrt{3}}{5}$x,
由$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{5}x}\\{y=-\frac{\sqrt{3}}{3}x+6\sqrt{3}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{45}{4}}\\{y=\frac{9\sqrt{3}}{4}}\end{array}\right.$,
∴$P({\frac{45}{4},\frac{9}{4}\sqrt{3}})$;
∴OP+PQ=OQ′=6$\sqrt{7}$
周长最小值是12+6$\sqrt{7}$.
(3)观察图象可知,只有点M在BC上时,存在OM=MN,如图:作MH⊥ON于H.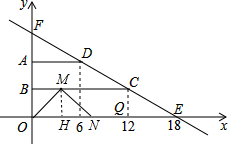
∵OM=MN,MH⊥ON,
∴OH=HN=BM=2t,
∴4t+t=12,
∴t=$\frac{12}{5}$.
∴t=$\frac{12}{5}$时,OM=MN.
点评 本题考查一次函数的应用、轴对称最短问题等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会利用对称解决最短问题,学会用方程的思想思考问题,属于中考常压轴题.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:填空题
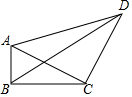 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5$\sqrt{2}$,则BD的长为$\sqrt{65}$.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5$\sqrt{2}$,则BD的长为$\sqrt{65}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
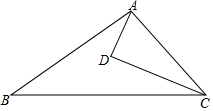 如图,已知D为△ABC内的一点,AD⊥CD,AB=2$\sqrt{3}$cm,AC=$\sqrt{8}$cm,AD=$\sqrt{3}$cm,BC=2CD.求凹四边形ABCD的面积.
如图,已知D为△ABC内的一点,AD⊥CD,AB=2$\sqrt{3}$cm,AC=$\sqrt{8}$cm,AD=$\sqrt{3}$cm,BC=2CD.求凹四边形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com