
【题目】如图,已知平行四边形ABCD及四边形外一直线l,四个顶点A、B、C、D到直线l的距离分别为a、b、c、d.
(1)观察图形,猜想得出a、b、c、d满足怎样的关系式?证明你的结论.
(2)现将l向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.

【答案】(1)a、b、c、d满足a+c=b+d(2)不一定成立.
【解析】试题分析:(1)此题可以连接平行四边形的对角线,交点是O.作OO1⊥l于O1.根据梯形的中位线定理得到2OO1=DD1+BB1=b+d=AA1+CC1=a+c.
(2)将l向上平移,分别有直线l过B点时;直线l过B点与D点之间时;直线l过D点时;直线l过C点与D点之间时;直线l过C点时;直线l过C点上方时.结合三角形的中位线定理和梯形的中位线定理进行分析.
试题解析:(1)a、b、c、d满足a+c=b+d.
证明:连接AC、BD,且AC、BD相交于点O,OO1为点O到O1的距离,
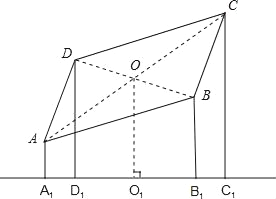
∴OO1为直角梯形BB1D1D的中位线,
∴2OO1=DD1+BB1=b+d;
同理:2OO1=AA1+CC1=a+c.
∴a+c=b+d.
(2)不一定成立.
分别有以下情况:
直线l过A点时,c=b+d;
直线l过A点与B点之间时,c﹣a=b+d;
直线l过B点时,c﹣a=d;
直线l过B点与D点之间时,a﹣c=b﹣d;
直线l过D点时,a﹣c=b;
直线l过C点与D点之间时,a﹣c=b+d;
直线l过C点时,a=b+d;
直线l过C点上方时,a+c=b+d.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图,一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在北偏东65°45′的方向上,渔船向正东方向航行l小时45分钟之后到达D点,观测到灯塔B恰好在正北方向上,已知两个灯塔之间的距离是12海里,渔船的速度是16海里/时,又知在灯塔C周围18.6海里内有暗礁,问这条渔船按原来的方向继续航行,有没有触礁的危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角坐标平面中,点![]() 在
在![]() 轴的负半轴上,直线
轴的负半轴上,直线![]() 经过点
经过点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 是点
是点![]() 关于原点的对称点,过点
关于原点的对称点,过点![]() 的直线
的直线![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,如果
,如果![]() .
.
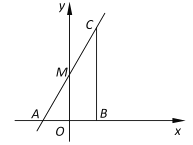
(1)求直线![]() 的表达式;
的表达式;
(2)如果点![]() 在直线
在直线![]() 上,且
上,且![]() 是等腰三角形,请求出点
是等腰三角形,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的社会实践活动中,第一小组负责调查全校10000名同学每天完成家庭作业时间情况,他们随机抽取了一部分同学进行调查,井绘制了所抽取样本的频数分布表和额数分布直方图(如图).
时间x(小时) | 频数 | 百分比 |
0.5≤x<1 | 4 | 8% |
1≤x<1.5 | 5 | 10% |
1.5≤x<2 | a | 40% |
2≤x<2.5 | 15 | 30% |
2.5≤x<3 | 4 | 8% |
x≥3 | 2 | b |
频数分布表

请根据图中信息解答下列问题:
(1)该小组一共抽查了___________人;
(2)频数分布表中的a=___________,b=____________;
(3)将频数分布直方图补充完整(直接画图,不写计算过程);
(4)《辽宁省落实教育部等九部门关于中小学生减负措施实施方案》规定,初中生每天书面家庭作业时间不超过1.5小时,根据表中数据,请你提出合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD不添加任何字母和数字,请你再添加一个条件∠1=∠2成立(要求给出三个答案),并选择其中一种情况加以证明.

条件1:________________________________;
条件2:________________________________;
条件3:________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )

A. ②③④ B. ①②③ C. ②③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com