
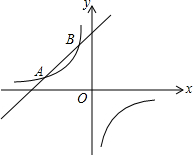
 如图,已知反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点(8,-$\frac{1}{2}$),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
如图,已知反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点(8,-$\frac{1}{2}$),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).分析 (1)分别把点A(8,-$\frac{1}{2}$)、B(m,4)代入反比例函数y1=$\frac{k}{x}$,可以得到k和m的值,再把B点坐标代入y2即可解决问题.
(2)当y1<y2时,根据反比例函数图象在下面即可写出x的范围.
解答  解:(1)∵反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点A(8,-$\frac{1}{2}$),
解:(1)∵反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点A(8,-$\frac{1}{2}$),
∴-$\frac{1}{2}$=$\frac{K}{8}$,
∴k=-4,
∴反比例函数解析式为y1=-$\frac{4}{x}$.
∵点B(m,4)在反比例函数解析式为y1=-$\frac{4}{x}$上,
∴4=-$\frac{4}{m}$,
∴m=-1,
又B(-1,4)在y2=x+b上,
∴4=-1+b,
∴b=5,
∴直线的解析式为y2=x+5.
(2)由图象可知,当y1<y2时x的取值范围-4<x<-1或x>0.
点评 本题考查反比例函数与一次函数有关知识,灵活掌握待定系数法求函数解析式,注意第二个问题容易漏解,考虑问题要全面,属于中考常考题型.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
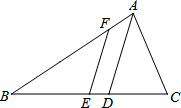 如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.
如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
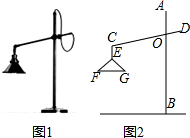 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
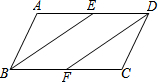 如图,在?ABCD中,若点E、F是AD、BC的中点,连接BE、DF.
如图,在?ABCD中,若点E、F是AD、BC的中点,连接BE、DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
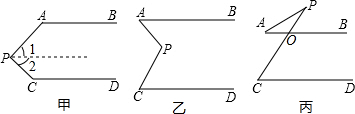 阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.
阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com