
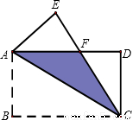
如图,将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F.
(1)求证:AF=CF;
(2)若AB=4,BC=6,求△AFC的面积.
(1)证明见解析;(2) .
.
【解析】
试题分析:(1)由折叠的性质可知∠ECA=∠BCA,由AD∥BC可知∠DAC=∠BCA,则∠ECA=∠DAC,可证AF=CF;
(2)根据(1)FC=FA,设FA=x,则FC=x,FD=6-x,在Rt△CDF中利用勾股定理得到关于x的方程x2=42+(6-x)2,解方程求出x,然后根据三角形的面积公式计算即可.
试题解析:(1)证明:由折叠的性质可知∠ECA=∠BCA,
由AD∥BC可知∠DAC=∠BCA,
∴∠ECA=∠DAC,
∴AF=CF;
(2)【解析】
∵四边形ABCD为矩形,
∴AD=BC=6,CD=AB=4,
由(1)知:FC=FA,
设FA=x,则FC=x,FD=6-x,
在Rt△CDF中,CF2=CD2+DF2,即x2=42+(6-x)2,解得x=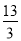 ,
,
∴折叠后的重叠部分的面积=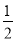 •AF•CD=
•AF•CD=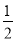 ×4×
×4×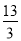 =
= .
.
考点:翻折变换(折叠问题).


科目:初中数学 来源:2015届北京市门头沟区八年级下学期期末考试数学试卷(解析版) 题型:选择题
一元二次方程4x2+x=1的二次项系数、一次项系数、常数项分别是( )
A.4,0,1 B.4,1,1 C.4,1,-1 D.4,1,0
查看答案和解析>>
科目:初中数学 来源:2015届北京市昌平区八年级下学期期末考试数学试卷(解析版) 题型:填空题
直线l1:y=kx与直线l2:y=ax+b在同一平面直角坐标系中的图象如图,则关于x的不等式ax+b>kx的解集为 .

查看答案和解析>>
科目:初中数学 来源:2015届北京市昌平区八年级下学期期末考试数学试卷(解析版) 题型:选择题
一次函数y=2x﹣3的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:填空题
如图,在直角坐标系中,正方形A1B1C1O、 A2B2C2C1、A3B3C3C2、…、AnBnCnCn-1的顶点A1、A2、A3、…、An均在直线y=kx+b上,顶点C1、C2、C3、…、Cn在x轴上,若点B1的坐标为(1,1),点B2的坐标为(3,2),那么点A4的坐标为 ,点An的坐标为 .
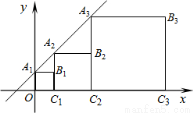
查看答案和解析>>
科目:初中数学 来源:2015届北京市房山区八年级下学期期末考试数学试卷(解析版) 题型:解答题
已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程x2﹣5x+4=0的两个根,点C在y轴正半轴上,且OB=2OC.
(1)试确定直线BC的解析式;
(2)求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:选择题
某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
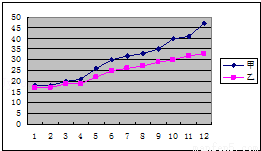
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差
B.甲运动员得分的中位数大于乙运动员得分的中位数
C.甲运动员的得分平均数大于乙运动员的得分平均数
D.甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com