
已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程x2﹣5x+4=0的两个根,点C在y轴正半轴上,且OB=2OC.
(1)试确定直线BC的解析式;
(2)求出△ABC的面积.

(1)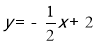 ;(2)3
;(2)3
【解析】
试题分析:(1)解方程x2﹣5x+4=0可求线段OA=1,OB=4,再确定A、B两点的坐标,根据OB=2OC,且点C在y轴正半轴上,求点C的坐标,然后根据待定系数法即可求得解析式;
(2)根据A、B的坐标求得AB的长,然后根据面积公式即可求得:
试题解析:(1)∵OA、OB的长是方程x2﹣5x+4=0的两个根,且OA<OB,
解得x1=4,x2=1,
∴OA=1,OB=4
∵A、B分别在x轴正半轴上,
∴A(1,0)、B(4,0),
又∵OB=2OC,且点C在y轴正半轴上
∴OC=2,C(0,2),
设直线BC的解析式为y=kx+b
∴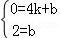 ,解得
,解得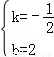
∴直线BC的解析式为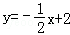 ;
;
(2)∵A(1,0)、B(4,0)
∴AB=3
∵OC=2,且点C在y轴上
∴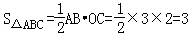 ;
;
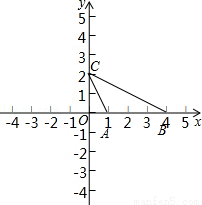
考点:1.待定系数法求一次函数解析式;2.一次函数图象上点的坐标特征.


科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:解答题
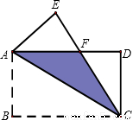
如图,将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F.
(1)求证:AF=CF;
(2)若AB=4,BC=6,求△AFC的面积.
查看答案和解析>>
科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:选择题
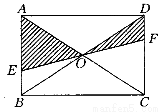
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( ).
A.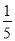 B.
B.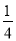 C.
C.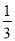 D.
D.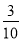
查看答案和解析>>
科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:选择题
在平面直角坐标系中,点P坐标为(4,-3),则点P在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中数学 来源:2015届北京市房山区八年级下学期期末考试数学试卷(解析版) 题型:选择题
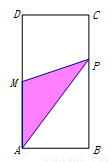
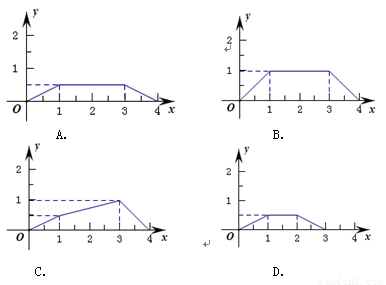
如图,矩形ABCD中,AB=1,AD=2,M是AD的中点,点P在矩形的边上,从点A出发,沿A→B→C→D运动,到达点D运动终止.设△APM的面积为y,点P经过的路程为x,那么能正确表示y与x之间函数关系的图象是( )
查看答案和解析>>
科目:初中数学 来源:2015届云南省八年级上学期期末考试数学试卷(解析版) 题型:解答题
你能化简( )(
)( )吗?我们不妨先从简单情况入手,现规律,归纳结论.
)吗?我们不妨先从简单情况入手,现规律,归纳结论.
(1)先填空:( )(
)( )= ;(
)= ;( )(
)( )= ; (
)= ; ( )(
)( )= ;……
)= ;……
由此猜想( )(
)( )= .
)= .
(2)利用这个结论,你能解决下面两个问题吗?
①2199+2198+2197+……+22+2+1;
②若 ,则
,则 等于多少?
等于多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com