
【题目】已知关于x的方程x2﹣(2k+3)x+k2=0有两个不相等的实数根x1 , x2 .
(1)求k的取值范围;
(2)若两不相等的实数根满足x1x2﹣x12﹣x22=﹣9,求实数k的值.
【答案】
(1)解:由已知可得,△=[﹣(2k+3)]2﹣41k2=12k+9>0
∴k>﹣ ![]()
(2)解:由已知可得x1+x2=2k+3,x1x2=k2,
∵x1x2﹣x12﹣x22=﹣9,
∴x1x2﹣[(x1+x2)2﹣2x1x2]=﹣9,
即3x1x2﹣(x1+x2)2=﹣9,
∴3k2﹣(2k+3)2=﹣9,
整理得k2+12k=0,解得k1=0,k2=﹣12,
又k>﹣ ![]() ,
,
∴k=0.
【解析】(1)根据判别式的意义得到△=[﹣(2k+3)]2﹣41k2=12k+9>0,然后解不等式即可;(2)根据根与系数的关系得到x1+x2=2k+3,x1x2=k2 , 再把x1x2﹣x12﹣x22=﹣9变形为即3x1x2﹣(x1+x2)2=﹣9,则3k2﹣(2k+3)2=﹣9,然后解关于k的方程,最后利用k的范围确定满足条件的k的值.
【考点精析】关于本题考查的求根公式和根与系数的关系,需要了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能得出正确答案.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,﹣2),点B(1,4)
(1)试建立相应的平面直角坐标系;
(2)描出线段AB的中点C,并写出其坐标;
(3)将线段AB沿水平方向向右平移3个单位长度得到线段A1B1,写出线段A1B1两个端点及线段中点C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )

A.24 B.12 C.6 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形中,一个内角α是另一个内角β的两倍时,我们称此三角形是“特征三角形”,其中α为“特征角”.如果一个“特征三角形”的“特征角”为102°,那么这个“特征三角形”的最小内角为___________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.同位角相等
B.同一平面内的两条不重合的直线有相交、平行和垂直三种位置关系
C.三角形的三条高线一定交于三角形内部同一点
D.三角形三条角平分线的交点到三角形三边的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC= ![]() .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 . 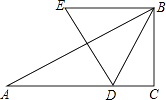
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com