
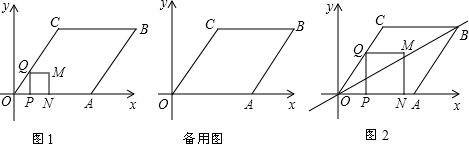
ЗжЮі ЃЈ1ЃЉИљОнСтаЮЕФаджЪЕУГіOA=OCЃЌдйИљОнШ§НЧКЏЪ§ЧѓГіЕуCЕФзјБъМДПЩЃЛ
ЃЈ2ЃЉИљОнУцЛ§ЙЋЪНСаГіКЏЪ§ЙиЯЕЪНЃЌзЂвтЖЏЕудЫЖЏЪБЕФМИжжЧщПіЃЌЕУГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉИљОнБЛЗжГЩЕФСНВПЗжжагавЛВПЗжЕФУцЛ§ЪЧСтаЮУцЛ§ЕФ$\frac{1}{5}$ЃЌЛГіЭМЪОЃЌЗжМИжжЧщПіНјааЬжТлНтД№ЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпСтаЮOABCжаЃЌOA=10ЃЌ
ЁрOC=10ЃЌ
ЁпcosЁЯCOA=$\frac{3}{5}$ЃЌ
ЁрЕуCЕФзјБъЮЊЃКЃЈ6ЃЌ8ЃЉЃЌ
ЁпЖЏЕуPДгЕуOГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮOAЗНЯђдЫЖЏЃЌ
ЁпOA=10ЃЌ
Ёрt=$\frac{30}{7}$ЪБЃЌNЕугыAЕужиКЯЃЛ
ЃЈ2ЃЉЂй$0ЃМtЁм\frac{30}{7}ЃЌS=\frac{16}{9}{t^2}$ЃЌ
Ђк$\frac{30}{7}ЃМtЁм6ЃЌS=-\frac{50}{27}{t^2}+\frac{280}{9}t-\frac{200}{3}$ЃЌ
Ђл$6ЃМtЁм8ЃЌS=-\frac{2}{3}{t^2}+\frac{8}{3}t-\frac{184}{3}$ЃЌ
Ђм8ЃМtЁм10ЃЌS=104-8tЃЛ
ЃЈ3ЃЉSСтаЮ=80ЃЌжБЯпOBЙ§дЕуЃЈ0ЃЌ0ЃЉЃЌBЕуЃЈ16ЃЌ8ЃЉЃЌЙЪжБЯпOBНтЮіЪНЮЊ$y=\frac{x}{2}$ЃЌ
жБЯпOBгыPQЁЂMNЗжБ№НЛгкEЁЂFЕуЃЌШчЭМЃК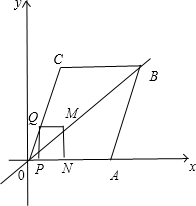
ЂйЕБ0ЃМtЁм6ЃЌ$EP=\frac{t}{2}$ЃЌ$EQ=\frac{5t}{6}$ЃЌ$FN=\frac{7t}{6}$ЃЌ$FM=\frac{t}{6}$ЃЌ
Шє${S_{ЫФБпаЮQEFN}}=\frac{1}{5}{S_{СтаЮ}}$ЃЌдђ$\frac{1}{2}ЃЈ\frac{5t}{6}+\frac{t}{6}ЃЉ•\frac{4t}{3}=16$ЃЌ${t_1}=2\sqrt{6}$ЃЌ
Шє${S_{ЫФБпаЮEPNF}}=\frac{1}{5}{S_{СтаЮ}}$ЃЌдђ$\frac{1}{2}ЃЈ\frac{t}{2}+\frac{7t}{6}ЃЉ•\frac{4t}{3}=16$ЃЌ${t_2}=\frac{6}{5}\sqrt{10}$ЃЌ
ЂкЕБ6ЃМtЁм8ЃЌ$EP=\frac{t}{2}$ЃЌ$EQ=8-\frac{t}{2}$ЃЌ$FN=\frac{t}{2}+4$ЃЌ$FM=4-\frac{t}{2}$ЃЌ
Шє${S_{ЫФБпаЮQEFN}}=\frac{1}{5}{S_{СтаЮ}}$ЃЌдђ$\frac{1}{2}ЃЈt+4ЃЉ•8=16$ЃЌt=0ЃЈЩсЃЉЃЌ
Шє${S_{ЫФБпаЮEPNF}}=\frac{1}{5}{S_{СтаЮ}}$ЃЌдђ$\frac{1}{2}ЃЈ12-tЃЉ•8=16$ЃЌt3=8ЃЛ
Ђл8ЃМtЁм10ЃЌВЛДцдкЗћКЯЬѕМўЕФtжЕЃЎ
ЕуЦР ДЫЬтПМВщЕФЪЧКЏЪ§злКЯЬтЃЌФбЖШБШНЯДѓЃЌЙиМќЪЧдЫгУЫФБпаЮЕФаджЪКЭУцЛ§ЙЋЪННјааЗжЮіЃЌзЂвтГіЯжЕФМИжжЧщПіЬжТлЃЌВЛФмТЉНтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
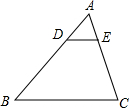 дкЁїABCжаЃЌDEЁЮBCЃЌШє$\frac{AD}{BD}=\frac{1}{2}$ЃЌ
дкЁїABCжаЃЌDEЁЮBCЃЌШє$\frac{AD}{BD}=\frac{1}{2}$ЃЌВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
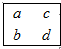 ШчЭМЪЧ2012Фъ11дТЗнЕФШеРњЃЌЯжгУвЛГЄЗНаЮдкШеРњжаШЮвтПђГі4ИіЪ§ЃЌЧыгУвЛИіЕШЪНБэЪОaЃЌbЃЌcЃЌdжЎМфЕФЙиЯЕЃЌЯТСаБэЪОе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ШчЭМЪЧ2012Фъ11дТЗнЕФШеРњЃЌЯжгУвЛГЄЗНаЮдкШеРњжаШЮвтПђГі4ИіЪ§ЃЌЧыгУвЛИіЕШЪНБэЪОaЃЌbЃЌcЃЌdжЎМфЕФЙиЯЕЃЌЯТСаБэЪОе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ| AЃЎ | a+d=b+c | BЃЎ | a+c=b+d | CЃЎ | a+b=c+d | DЃЎ | a+d+1=b+c |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
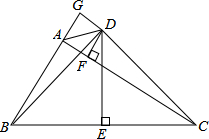 ШчЭМЃЌдкЁїABCжаЃЌACЃОABЃЌDEЃЈЕуDдкЁїABCЕФЭтВПЃЉДЙжБЦНЗжBCЃЌНЛBCгкЕуEЃЌСЌНгBDЃЌCDЃЌADЃЌЙ§ЕуDзїDFЁЭACгкЕуFЃЌбгГЄBAЕНЕуGЃЌЪЙЕУBG=CFЃЌСЌНгDGЃЌШєЁЯDBC-ЁЯGBD=ЁЯBCAЃЌдђЯТСаЫЕЗЈжаВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкЁїABCжаЃЌACЃОABЃЌDEЃЈЕуDдкЁїABCЕФЭтВПЃЉДЙжБЦНЗжBCЃЌНЛBCгкЕуEЃЌСЌНгBDЃЌCDЃЌADЃЌЙ§ЕуDзїDFЁЭACгкЕуFЃЌбгГЄBAЕНЕуGЃЌЪЙЕУBG=CFЃЌСЌНгDGЃЌШєЁЯDBC-ЁЯGBD=ЁЯBCAЃЌдђЯТСаЫЕЗЈжаВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ| AЃЎ | ЁЯBGD=90Ёу | BЃЎ | ADЦНЗжЁЯGAC | CЃЎ | ЁЯGDB=ЁЯFDC | DЃЎ | ЁЯBDG=90Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
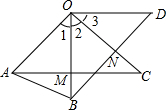 вбжЊЃЌOA=OBЃЌOC=ODЃЌЁЯ1=ЁЯ2=ЁЯ3ЃЌACНЛOBгкMЃЌBDНЛOCгкNЃЌЧѓжЄЃКOM=ONЃЎ
вбжЊЃЌOA=OBЃЌOC=ODЃЌЁЯ1=ЁЯ2=ЁЯ3ЃЌACНЛOBгкMЃЌBDНЛOCгкNЃЌЧѓжЄЃКOM=ONЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com