
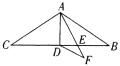
【题目】如图,△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是△ABD的角平分线,DF∥AB交AE延长线于F,则DF的长为 .
【答案】![]()
【解析】
试题根据等腰三角形三线合一的性质可得到AD⊥BC,∠BAD=∠CAD,从而可得到∠BAD=60°,∠ADB=90°,再根据角平分线的性质即可得到∠DAE=∠EAB=30°,从而可推出AD=DF,根据直角三角形30度角的性质即可求得AD的长,即得到了DF的长.
∵△ABC是等腰三角形,D为底边的中点,
∴AD⊥BC,∠BAD=∠CAD,
∵∠BAC=120°,
∴∠BAD=60°,∠ADB=90°,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB=30°.
∵DF∥AB,
∴∠F=∠BAE=30°.
∴∠DAF=∠F=30°,
∴AD=DF.
∵AB=9,∠B=30°,
∴AD=![]() ,
,
∴DF=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ![]() ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )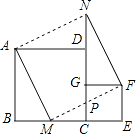
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
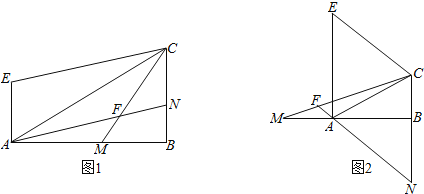
【题目】Rt△ABC中,∠ABC=90°,在直线AB上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)如图1,若点M在线段AB边上时,求∠AFM的度数;
(2)如图2,若点M在线段BA的延长线上时,且∠CMB=15°,求∠AFM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,矩形OABC的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①. 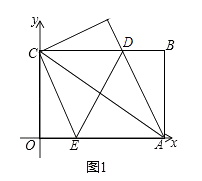
(1)求点D的坐标和AD所在直线的函数关系式;
(2)⊙M的圆心M始终在直线AC上(点A除外),且⊙M始终与x轴相切,如图②. 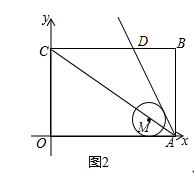
①求证:⊙M与直线AD相切;
②圆心M在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时⊙M与x轴、y轴和直线AD都相切时的圆心M的坐标;如果不能相切,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】县内某小区正在紧张建设中,现有大量的沙石需要运输,“建安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“建安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“建安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
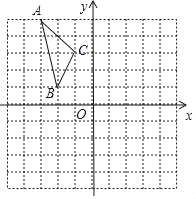
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC和△A1B1C1关于原点O对称,画出△A1B1C1,并写出△A1B1C1的各顶点的坐标;
(2)将△ABC绕着点O按顺时针方向旋转90°得到的△A2B2C2,画出△A2B2C2,并写出△A2B2C2的各顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com