
【题目】Rt△ABC中,∠ABC=90°,在直线AB上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)如图1,若点M在线段AB边上时,求∠AFM的度数;
(2)如图2,若点M在线段BA的延长线上时,且∠CMB=15°,求∠AFM的度数.
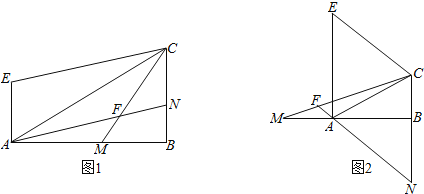
【答案】(1) 45°;(2) 120°.
【解析】
(1)如图1,连接EM.根据AE⊥AB,AE=MB,AM=CB,可求出△AEM≌△BMC;根据直角三角形的性质可知△EMC是等腰直角三角形;再结合平行线的性质可知∠AFM=45°.
(2)如图2,连接EM.同(1)△AEM≌△BMC,则EM=MC,∠MEA=∠CMB=15°.易证△EMC是等边三角形,故∠ECM=60°,又由AN∥CE得到:∠AFM=∠ECM=60°.
(1)连接EM.
∵AE⊥AB,∴∠EAM=∠B=90°.
在△AEM与△BMC中,
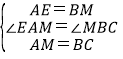 ,
,
∴△AEM≌△BMC(SAS).
∴∠AEM=∠BMC,EM=MC.
∵∠AEM+∠AME=90°,
∴∠BMC+∠AME=90.
∴∠EMC=90°.
∴△EMC是等腰直角三角形.
∴∠MCE=45°
∵AN∥CE,
∴∠AFM=∠MCE=45°;
(2)如图2,连接ME.
同(1)△AEM≌△BMC(SAS),则EM=MC,∠MEA=∠CMB=15°.
又∵∠MEA+∠EMA=90°,
∴∠EMC=60°,
∴△EMC是等边三角形,
∴∠ECM=60°,
∵AN∥CE
∴∠AFM+∠ECM=180°,
∴∠AFM=120°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
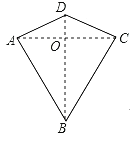
【题目】两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中 AB=CB,AD=CD,詹姆斯在探究筝形的性质时,得到如下结论:① ACBD;②AOCO![]() AC;③△ABD≌△CBD;④四边形ABCD的面积=
AC;③△ABD≌△CBD;④四边形ABCD的面积=![]() ACBD,其中,正确的结论有_____.
ACBD,其中,正确的结论有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在平时的练习中,遇到下面一道题目:
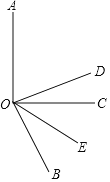
如图,∠AOC=90°,OE 平分∠BOC,OD平分∠AOB.
①若∠BOC=60°,求∠DOE 度数;
②若∠BOC=α(0<α<90°),其他条件不变,求∠DOE 的度数.
(1)下面是某同学对①问的部分解答过程,请你补充完整.
∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ,
∵OD 平分∠AOB,
∴ ,(角平分线的定义)
∴∠DOE= .
(注:符号∵表示因为,用符号∴表示所以).
(2)仿照①的解答过程,完成第②小题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
(1)求∠B的度数;
(2)如果AC=3cm,CD=![]() cm,求△ABD的面积.
cm,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为地铁调价后的计价表.调价后小明、小伟从家到学校乘地铁分别需要4元和3元.由于刷卡坐地铁有优惠,因此,他们平均每次实付3.6元和2.9元.已知小明从家到学校乘地铁的里程比小伟从家到学校的里程多5 km,且小明每千米享受的优惠金额是小伟的2倍,求小明和小伟从家到学校乘地铁的里程分别是多少千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里(将各数用逗号分开):﹣4,0.62, ![]() ,18,0,﹣8.91,+100
,18,0,﹣8.91,+100
正数:{______…};负数:{______…};整数:{______…};分数:{______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是△ABD的角平分线,DF∥AB交AE延长线于F,则DF的长为 .
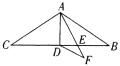
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com