
【题目】已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
(1)求∠B的度数;
(2)如果AC=3cm,CD=![]() cm,求△ABD的面积.
cm,求△ABD的面积.

【答案】(1)∠B=30°;(2)3![]() cm2.
cm2.
【解析】
(1)根据已知条件得到AD=BD,由等腰三角形的性质得到∠B=∠DAE,根据AD是△ABC的角平分线,求得∠DAE=∠DAC,于是得到∠B=∠DAE=∠DAC,列方程即可得到结论;
(2)根据已知条件求得Rt△ACD≌Rt△AED,根据全等三角形的性质得到AE=AC,DE=CD,于是得到AB,即可得到结论.
(1)∵DE⊥AB且AE=BE,
∴AD=BD,
∴∠B=∠DAE,
∵AD是△ABC的角平分线,
∴∠DAE=∠DAC,
∴∠B=∠DAE=∠DAC,
∵∠C=90°,
∴∠B+∠DAE+∠DAC=90°,
∴∠B=30°;
(2)∵∠C=90°,AD是△ABC的角平分线,DE⊥AB,
在Rt△ACD与Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED,(HL),
∴AE=AC=3cm,DE=CD=![]() cm,
cm,
∵AE=BE,
∴AB=2AE=2×3=6,
∴S△ABD=![]() ABDE=
ABDE=![]() ×6×
×6×![]() =3
=3![]() cm2.
cm2.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
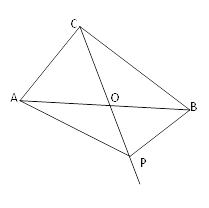
【题目】如图,在△ABC中,AB=2,AO=BO,P是直线CO上的一个动点,∠AOC=60°,当△PAB是以BP为直角边的直角三角形时,AP的长为( )
A. ![]() ,1,2 B.
,1,2 B. ![]() ,
,![]() ,2 C.
,2 C. ![]() ,
,![]() ,1 D.
,1 D. ![]() ,2
,2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ![]() ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )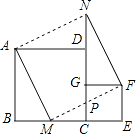
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
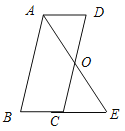
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
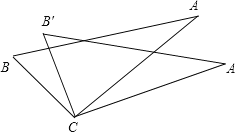
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,在直线AB上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)如图1,若点M在线段AB边上时,求∠AFM的度数;
(2)如图2,若点M在线段BA的延长线上时,且∠CMB=15°,求∠AFM的度数.
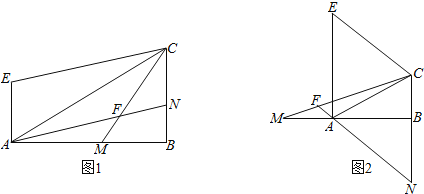
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,矩形OABC的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①. 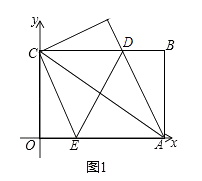
(1)求点D的坐标和AD所在直线的函数关系式;
(2)⊙M的圆心M始终在直线AC上(点A除外),且⊙M始终与x轴相切,如图②. 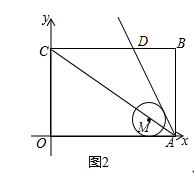
①求证:⊙M与直线AD相切;
②圆心M在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时⊙M与x轴、y轴和直线AD都相切时的圆心M的坐标;如果不能相切,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com