
【题目】某同学在平时的练习中,遇到下面一道题目:
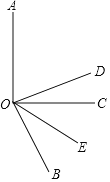
如图,∠AOC=90°,OE 平分∠BOC,OD平分∠AOB.
①若∠BOC=60°,求∠DOE 度数;
②若∠BOC=α(0<α<90°),其他条件不变,求∠DOE 的度数.
(1)下面是某同学对①问的部分解答过程,请你补充完整.
∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ,
∵OD 平分∠AOB,
∴ ,(角平分线的定义)
∴∠DOE= .
(注:符号∵表示因为,用符号∴表示所以).
(2)仿照①的解答过程,完成第②小题.
【答案】(1)45°;(2)45°.
【解析】
(1)根据∠AOC、∠BOC的度数可得出∠AOB的度数,根据角平分线的定义即可得出∠BOE、∠BOD的度数,再根据∠DOE与∠BOE、∠BOD之间的关系通过角的计算即可得出结论;
(2)根据∠AOC、∠BOC的度数可得出∠AOB的度数,根据角平分线的定义即可得出∠BOE、∠BOD的度数,再根据∠DOE与∠BOE、∠BOD之间的关系通过角的计算即可得出结论.
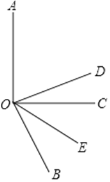
(1) ∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= 30° . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ∠AOB=150° ,
∵OD 平分∠AOB,
∴ ∠BOD=75° ,(角平分线的定义)
∴∠DOE= 45° .
(2)
∵OE 平分∠BOC,∠BOC=α.
∴∠BOE=![]() (角平分线的定义)
(角平分线的定义)
∵∠AOC=90°,∠BOC=α
∴![]() ,
,
∵OD 平分∠AOB,
∴∠BOD=![]() ,(角平分线的定义)
,(角平分线的定义)
∴∠DOE=45°.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a= ,b= ;
)2,用含m、n的式子分别表示a、b,得a= ,b= ;
(2)试着把7+4![]() 化成一个完全平方式.
化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B、C三地,A地在B、C两地之间.甲、乙两辆汽车分别从B、C两地同时出发,沿这条公路匀速相向行驶,甲匀速行驶1小时到达A地后继续以相同的速度向C处行驶,到达C后停止,乙匀速行驶1.2小时后到达A地并停止运动,甲、乙两车离A地的距离y1、y2(千米)与行驶时间x(时)的函数关系如图所示.
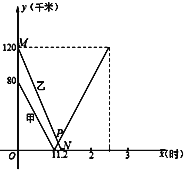
(1)BC的距离为 km
⑵求线段MN的函数表达式;
⑶求点P的坐标,并说明点P的实际意义;
⑷出发多长时间后,甲、乙相距60km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ![]() ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )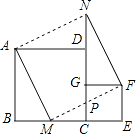
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为点 D.下列说法中:①∠B的余角只有∠BAD;②∠B=∠C;③线段 AB 的长度表示点 B 到直线 AC 的距离;④AB·AC=BC·AD;一定正确的有( )
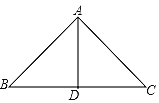
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
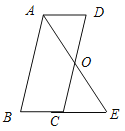
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
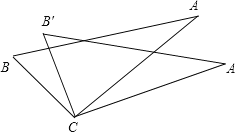
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
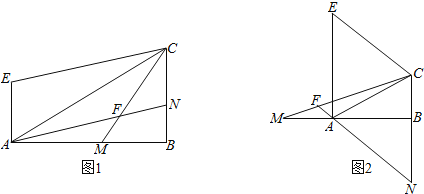
【题目】Rt△ABC中,∠ABC=90°,在直线AB上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)如图1,若点M在线段AB边上时,求∠AFM的度数;
(2)如图2,若点M在线段BA的延长线上时,且∠CMB=15°,求∠AFM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com