
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a= ,b= ;
)2,用含m、n的式子分别表示a、b,得a= ,b= ;
(2)试着把7+4![]() 化成一个完全平方式.
化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:![]() .
.
科目:初中数学 来源: 题型:
【题目】宿州市高新区某电子电路板厂到安徽大学从2018年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4、P5、P6,…,则点P2018的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x=2,则2|x|-1=3.以上命题是真命题的有( ).
A. ①②③④ B. ①④ C. ②④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上填写理由,完成下面的证明. 如图,已知∠1+∠2=180°,∠B=∠3,求证∠C=∠AED
证明:∵∠1+∠2=180°(已知),∠1+∠DFE=180°()
∴∠2=∠DFE()
∴AB∥EF()
∴∠3=∠ADE()
又∵∠B=∠3(已知)
∴∠B=∠ADE()
∴DE∥BC()
∴∠C=∠AED()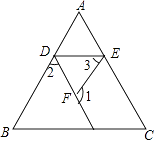
查看答案和解析>>
科目:初中数学 来源: 题型:
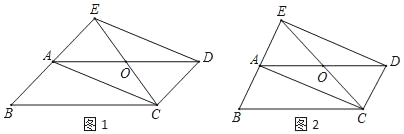
【题目】已知:在平行四边形ABCD中,点O是边AD的中点,连接CO并延长交BA延长线于点E,连接ED、AC.
(1)如图1,求证:四边形AEDC是平行四边形;
(2)如图2,若四边形AEDC是矩形,请探究∠COD与∠B的数量关系,写出你的探究结论,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
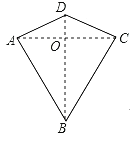
【题目】两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中 AB=CB,AD=CD,詹姆斯在探究筝形的性质时,得到如下结论:① ACBD;②AOCO![]() AC;③△ABD≌△CBD;④四边形ABCD的面积=
AC;③△ABD≌△CBD;④四边形ABCD的面积=![]() ACBD,其中,正确的结论有_____.
ACBD,其中,正确的结论有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
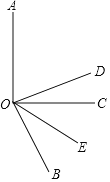
【题目】某同学在平时的练习中,遇到下面一道题目:
如图,∠AOC=90°,OE 平分∠BOC,OD平分∠AOB.
①若∠BOC=60°,求∠DOE 度数;
②若∠BOC=α(0<α<90°),其他条件不变,求∠DOE 的度数.
(1)下面是某同学对①问的部分解答过程,请你补充完整.
∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ,
∵OD 平分∠AOB,
∴ ,(角平分线的定义)
∴∠DOE= .
(注:符号∵表示因为,用符号∴表示所以).
(2)仿照①的解答过程,完成第②小题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com