
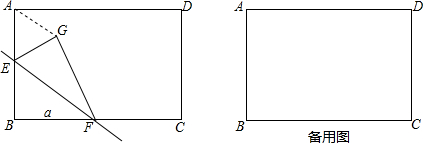
分析 (1)如图,当点G对角线AC上时,AG有最小值,由翻折的性质可得GF=GC=BC=BF=a,由勾股定理得即可得到结论;
(2)把CG=BF=4时,代入$\sqrt{{a}^{2}+9}$-a可得结果.
解答 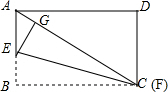 解:(1)如图,当点G对角线AC上时,AG有最小值,
解:(1)如图,当点G对角线AC上时,AG有最小值,
由翻折的性质可得GF=GC=BC=BF=a,
由勾股定理得,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{B{F}^{2}+A{B}^{2}}$=$\sqrt{{a}^{2}+9}$,
∴AG=AC-GC=$\sqrt{{a}^{2}+9}$-a,
故答案为:$\sqrt{{a}^{2}+9}$-a.
(2)当CG=BF=4时,
即a=4时,AG 的最小值=$\sqrt{{a}^{2}+9}$-a=5-4=1,
故答案为:a=4时 AG=1.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,本题判断出符合要求的点B′的位置是解题的关键,也是难点.


科目:初中数学 来源: 题型:选择题
| A. | 一条弦把圆分为两条弧,这两条弧不可能是等弧 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 长度相等的两条弧是等弧 | |
| D. | 经过圆心的每条直线都是圆的对称轴 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
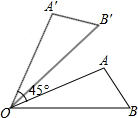 如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.
如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com