练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】有A，B，C三种款式的帽子，E，F二种款式的围巾，穿戴时小婷任意选一顶帽子和一条围巾．

    （1）用合适的方法表示搭配的所有可能性结果．

    （2）求小婷恰好选中她所喜欢的A款帽子和E款围巾的概率．

    【答案】（1）有A.E，A.F，B.E，B.F，C.E，C.F，6种情况；（2）.

    【解析】试题分析：（1）根据题意，使用列举法，可得小明任意选取一件衣服和一条裤子的情况数目，进而按概率的计算公式计算可得答案．

    （2）由（1）即可求出小婷恰好选中她所喜欢的A款帽子和E款围巾的概率．

    试题解析：（1）根据题意，小婷任意选取一顶帽子和一条围巾，有A.E，A.F，B.E，B.F，C.E，C.F，6种情况。

    （2）小婷恰好选中她所喜欢的A款帽子和E款围巾的概率=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在边BC上以每秒1个单位长的速度由点C向点B运动．

    （1）当t为何值时，四边形PODB是平行四边形？

    （2）在线段PB上是否存在一点Q，使得ODQP为菱形？若存在，求t的值；若不存在，请说明理由；

    （3）△OPD为等腰三角形时，写出点P的坐标（不必写过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC延长线于M，连接CD，下列四个结论：①∠ADC=45°；②BD=AE；③AC+CE=AB；④AB-BC=2MC，其中正确的有（ ）个.

    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，

    （1）求∠APO+∠DCO的度数；

    （2）求证：AC=AO+AP.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是边长为1的正方形，点E在AD边上运动，且不与点A和点D重合，连结CE，过点C作CF⊥CE交AB的延长线于点F，EF交BC于点G．

    （1）求证：△CDE≌△CBF；

    （2）当DE=时，求CG的长；

    （3）连结AG，在点E运动过程中，四边形CEAG能否为平行四边形？若能，求出此时DE的长；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展.小明计划给朋友快递一部分物品，经了解甲、乙两家快递公司比较合适，甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费，乙公司表示：按每千克16元收费，另加包装费3元.设小明快递物品x千克.

    (1)当x＞1时，请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式；

    (2)在(1)的条件下，小明选择哪家快递公司更省钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，AB=2，∠DAB=60°,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.

    （1）求证：四边形AMDN是平行四边形；

    （2）填空：①当AM的值为 时，四边形AMDN是矩形；②当AM的值为 时，四边形AMDN是菱形。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD=CB，延长CD交BA的延长线于点E．

    （1）求证：CD为⊙O的切线；

    （2）若BD的弦心距OF=1，∠ABD=30°，求图中阴影部分的面积．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一个正方形甲和两个正方形乙分别沿着图中虚线川剪刀剪成4个完全相等的长方形和一个正方形（如图1），已知正方形甲中剪出的小正方形面积是1，正方形乙中剪出的小正方形面积是4，现将剪得的12个长方形摆成如图2正方形（不重叠无缝隙）．则正方形的面积是（）

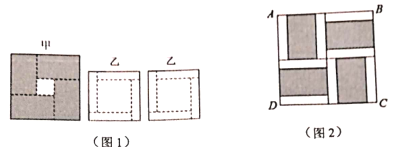
    A.9B.16C.25D.36

    查看答案和解析>>

    同步练习册答案