
【题目】把一副三角板的直角顶点O重叠在一起.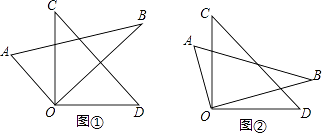
(1)问题发现:如图①,当OB平分∠COD时,∠AOD+∠BOC的度数是;
(2)拓展探究:如图②,当OB不平分∠COD时,∠AOD+∠BOC的度数是多少?
(3)问题解决:当∠BOC的余角的4倍等于∠AOD时,求∠BOC的度数.
【答案】
(1)180°
(2)解:∵∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,
∴∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=90°+90°=180°.
(3)解:∵由(1)、(2)得,∠AOD+∠BOC=180°,
∴∠AOD=180°﹣∠BOC.
∵∠AOD=4(90°﹣∠BOC),
∴180°﹣∠BOC=4(90°﹣∠BOC),
∴∠BOC=60°.
【解析】解:(1)∵OB平分∠COD,∠COD =90°,
∴∠BOC=∠BOD=45°,
∵∠AOC+∠BOC=45°,
∴∠AOC=45°,
∴∠AOD+∠BOD=∠AOC+∠COD+∠BOC=45°+90°+45°=180°.
【考点精析】本题主要考查了角的平分线和角的运算的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的高,BF∥AC,过D点的直线交AC于点E,交BF于点F,DE=DF. 求证: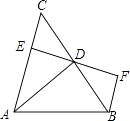
(1)AB=AC;
(2)BC平分∠ABF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE(如图①),连接AD,BE,易证明BE=AD.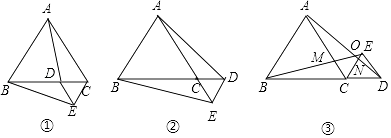
(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由;
(2)在图②中,若等边三角形CDE与等边三角形ABC均在直线BC的同一侧(如图③),并且B,C,D三点在同一直线上,猜想BE=AD是否依然成立?试说明理由;
(3)在(2)的条件下,根据图汇总所标字母,请直接写出你发现的两个正确结论.
①;② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( ) 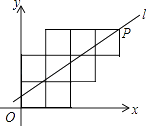
A.![]()
B.y= ![]() x+
x+ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
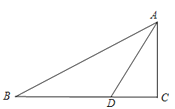
【题目】如图,已知在Rt△ABC中,∠C=900,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D在AB上,BC=BD,DE⊥AB交AC于点E,△ABC的周长为12,△ADE的周长为6,则BC的长为( ) 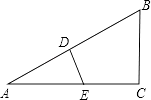
A.3
B.4
C.5
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com