
【题目】如图,以正方形ABCD的一边向形外作等边△ABE,BD与EC交于点F,则∠AFD等于( )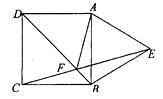
A.60°
B.50°
C.45°
D.40°
【答案】A
【解析】解:∵四边形ABCD是正方形.
∴AD=CD,∠ADF=∠CDF=45°.
∴△ADF与△CDF全等.
∴∠AFD=∠CFD.
∵CB=CE,∴∠BCE=∠CEB.
∵∠CBE=∠ABC+∠ABE=90°+60°=150°,
∴∠BCE=15°.
∵∠CBD=45°,
∴∠CFD=∠CBD+∠BCE=60°.
∴∠AFD=60°.
故选A.
【考点精析】利用等边三角形的性质和正方形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
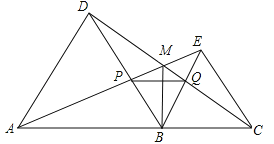
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
港口 | 运费(元/吨) | |
甲库 | 乙库 | |
A港 | 14 | 20 |
B港 | 10 | 8 |
(1)设从甲仓库运送到A港口的物资为x吨,用含x的式子填写下表:
港口 | 运费(元/吨) | |
甲库 | 乙库 | |
A港 | x | |
B港 | ||
(2)求总费用y(元)与x(箱)之间的函数关系式,并写出x的取值范围;
(3)求出最低费用,并说明费用最低时的调配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板的直角顶点O重叠在一起.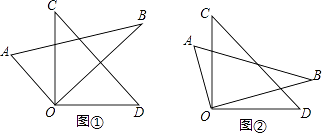
(1)问题发现:如图①,当OB平分∠COD时,∠AOD+∠BOC的度数是;
(2)拓展探究:如图②,当OB不平分∠COD时,∠AOD+∠BOC的度数是多少?
(3)问题解决:当∠BOC的余角的4倍等于∠AOD时,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是 时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是 时,它们一定不全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)29×20.18+72×20.18+13×20.18-14×20.18;
(2)1002-992+982-972+…+42-32+22-12.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B= ![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com