
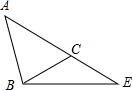
 如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.
如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长. 分析 作AM⊥BC,CN⊥BN,根据等腰三角形的性质求出BC的长,证明CN∥AB,根据平行线的性质,得到成比例线段,求出NE的长,得到答案.
解答 解:作AM⊥BC,CN⊥BN,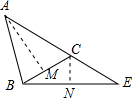
∵AB=AC,∠CBE=$\frac{1}{2}$∠A,
∴∠BAM=$\frac{1}{2}$∠A=∠CBE,
∴BM=MC=5×$\frac{\sqrt{5}}{5}$=$\sqrt{5}$,
∴BC=2$\sqrt{5}$,CN=2$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=2,
∴BN=$\sqrt{{BC}^{2}-C{N}^{2}}$=4,
易知∠1=∠2∴∠NEC=∠BAC,
∴CN∥AB,
∴$\frac{2}{5}$=$\frac{NE}{4+NE}$,得NE=$\frac{8}{3}$,
∴BE=4+$\frac{8}{3}$=$\frac{20}{3}$,
∴BC=2$\sqrt{5}$,BE=$\frac{20}{3}$.
点评 本题考查的是解直角三角形的知识,正确作出辅助线,构造直角三角形运用锐角三角函数进行解答是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
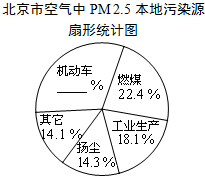 据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:
据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$或-$\sqrt{2}$ | B. | $\sqrt{2}$或-$\sqrt{2}$ | C. | 2或-$\sqrt{2}$ | D. | $\frac{3}{2}$或-$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 快、慢两车分别从相距120千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,立即按原路返回,返回时的速度是去时速度的2倍,结果与慢车同时回到甲地.慢车距出发地的路程y1(千米)与出发后所用的时间x(小时)的关系如图所示.
快、慢两车分别从相距120千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,立即按原路返回,返回时的速度是去时速度的2倍,结果与慢车同时回到甲地.慢车距出发地的路程y1(千米)与出发后所用的时间x(小时)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
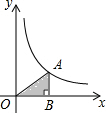 如图,在平面直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )
如图,在平面直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 先增大后减小 | D. | 不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com