
分析 首先求出使关于x的方程(a+2)x2+2ax+1=0有解的a的范围,再求出不等式组$\left\{\begin{array}{l}{x+2≤a}\\{2a+x>1}\end{array}\right.$无解的范围,进而得到同时满足这两个条件的a的取值范围,然后利用概率公式求解即可.
解答 解:关于x的方程(a+2)x2+2ax+1=0有解时,
a+2=0或a+2≠0,且△=4a2-4(a+2)≥0,
解得a≤-1,或a≥2,
∵不等式组$\left\{\begin{array}{l}{x+2≤a}\\{2a+x>1}\end{array}\right.$无解,
∴1-2a≥a-2,
∴a≤1.
由题意得a≤-1,
∴a=-2,-1,
∴使关于x的方程(a+2)x2+2ax+1=0有解,且不等式组$\left\{\begin{array}{l}{x+2≤a}\\{2a+x>1}\end{array}\right.$无解的概率为$\frac{2}{6}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 此题考查了概率公式的应用、根的判别式以及解一元一次不等式组.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
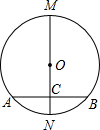 如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
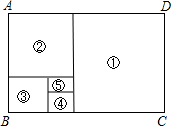 如图,在“黄金矩形”ABCD(即$\frac{宽AB}{长BC}$≈0.618)中,依次画正方形①、②、③、④
如图,在“黄金矩形”ABCD(即$\frac{宽AB}{长BC}$≈0.618)中,依次画正方形①、②、③、④查看答案和解析>>
科目:初中数学 来源: 题型:解答题
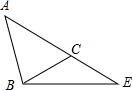 如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.
如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则a2>ab | B. | 若$\sqrt{(1-m)^{2}}$=m-1,则m≤1 | ||
| C. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | D. | 已知a,b为实数,若a+b=1,则ab≤$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
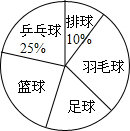 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:| 球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
| 人数 | a | 12 | 36 | 18 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com