Question

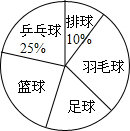
4．某中学为合理安排体育活动，在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中，随机抽取了若干名学生进行调查，了解学生最喜爱的一种球类运动，每人只能在这五种球类运动中选择一种．调查结果统计如下：

球类名称	乒乓球	排球	羽毛球	足球	篮球
人数	a	12	36	18	b

解答下列问题：
（1）a=30，b=24；
（2）试估计上述500名学生中最喜欢羽毛球运动的人数；
（3）该学校将组织趣味运动会，九（1）班决定从3名喜欢乒乓球、1名喜欢羽毛球，1名喜欢篮球的5名学生中随机抽取2人作为班级代表参加活动，那么被抽到的2名同学都是喜欢乒乓球的概率是多少？请用树状图或列表法说明理由．

Answer 1

分析 （1）首先用喜欢排球的人数除以其所占的百分比即可求得样本容量；再用样本容量乘以乒乓球所占的百分比即可求得a，用样本容量减去其他求得b值；
（2）用总人数乘以喜欢羽毛球的人所占的百分比即可；
（3）设3名喜欢乒乓球、1名喜欢羽毛球，1名喜欢篮球的分别为红1，红2，红3，绿1，绿2，通过列表即可求出被抽到的2名同学都是喜欢乒乓球的概率．

解答 解：（1）∵喜欢排球的有12人，占10%，
∴样本容量为12÷10%=120；
∴a=120×25%=30人，b=120-30-12-36-18=24人；
故答案为：a=30，b=24；           
（2）500×$\frac{36}{120}$=150（人）；
（3）设3名喜欢乒乓球、1名喜欢羽毛球，1名喜欢篮球的分别为红1，红2，红3，绿1，绿2，列表如下：

	红1	红2	红3	绿1	绿2
红1		（红1，红2）	（红1，红3）	（红1，绿1 ）	（红1，绿2）
红2	（红2，红1）		（红2，红3）	（红2，绿1）	（红2，绿2）
红3	（红3，红1）	（红3，红2）		（红3，绿1）	（红3，绿2）
绿1	（绿1，红1）	（绿1，红2）	（绿1，红3）		（绿1，绿2）
绿2	（绿2，红1）	（绿2，红2）	（绿2，红3）	（绿2，绿1）

∵共20种等可能的结果，其中被抽到的2名同学都是喜欢乒乓球的有6种等可能情况，
∴P=$\frac{6}{20}=\frac{3}{10}$．

点评 此题考查了树状图法与列表法求概率以及条形统计图与扇形统计图．用到的知识点为：概率=所求情况数与总情况数之比．