
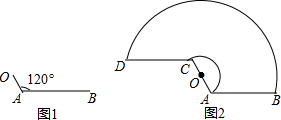
分析 (1)利用已知图形得出雨刮杆AB旋转的最大角度,再利用锐角三角函数关系得出BE的长,进而求出BO的长;
(2)直接得出△BAO≌△OCD,进而得出雨刮杆AB扫过的最大面积.
解答 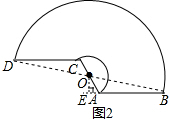 解:(1)雨刮杆AB旋转的最大角度为180°,
解:(1)雨刮杆AB旋转的最大角度为180°,
如图2,连接OB,过O点作AB的垂线交BA的延长线于E,
∵∠OAB=120°,∴∠OAE=60°
在Rt△OAE中,
∵∠OAE=60°,OA=10cm,
∴sin∠OAE=$\frac{OE}{OA}$=$\frac{OE}{10}$,
∴OE=5$\sqrt{3}$cm,AE=5cm
∴EB=AE+AB=50cm,
在Rt△OEB中,
∵OE=5$\sqrt{3}$cm,EB=50cm,
∴OB=$\sqrt{O{E^2}+B{E^2}}$=$\sqrt{2575}$=$5\sqrt{103}$(cm);
(2)∵雨刮杆AB旋转180°得到CD,即△OCD与△OAB关于点O中心对称,
∴△BAO≌△OCD,
∴S△BAO=S△OCD,
∴雨刮杆AB扫过的最大面积S=$\frac{1}{2}$π(OB2-OA2)=1237.5π(cm2).
点评 此题主要考查了勾股定理的应用以及锐角三角函数关系,利用锐角三角函数关系得出OE的长是解题关键.


科目:初中数学 来源: 题型:解答题
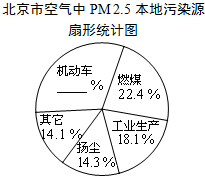 据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:
据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$x(x+1)=45 | B. | $\frac{1}{2}$x(x-1)=45 | C. | x(x+1)=45 | D. | x(x-1)=45 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
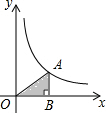 如图,在平面直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )
如图,在平面直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 先增大后减小 | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com