
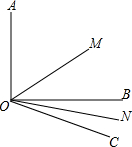
 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;分析 (1)根据角平分线的以求出∠MOC与∠NOC的度数,然后相减即可求出∠MON的度数;
(2)根据(1)的求解思路,先利用角平分线的定义表示出∠MOC与∠NOC的度数,然后相减即可得到∠MON的度数;
解答 解:(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×120°=60°,
∠NOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×30°=15°,
∴∠MON=∠MOC-∠NOC=60°-15°=45°;
故答案为:45;
(2)能.
∵∠AOB=90°,∠BOC=2x°,
∴∠AOC=90°+2x°
∵OM、ON分别平分∠AOC,∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(90°+2x°)=45°+x,
∴∠CON=$\frac{1}{2}$∠BOC=x,
∴∠MON=∠MOC-∠CON=45°+x-x=45°.
点评 此题主要考查学生对角的计算的理解和掌握,此题难度不大,属于基础题,但是此题中涉及到两种情况,具有很好的代表性和典型性,是一道好题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
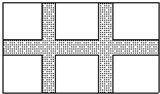 如图,在宽为20m,长为32m的矩形耕地上,修筑宽度一样的三条道路(如图),把耕地分成大小相等的六块作为实验田,要使实验田面积为504m2,求每条道路的宽度为多少米?
如图,在宽为20m,长为32m的矩形耕地上,修筑宽度一样的三条道路(如图),把耕地分成大小相等的六块作为实验田,要使实验田面积为504m2,求每条道路的宽度为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠ABM为直角,点C为线段BA的中点,点D为射线BM上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于点F.
如图,∠ABM为直角,点C为线段BA的中点,点D为射线BM上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
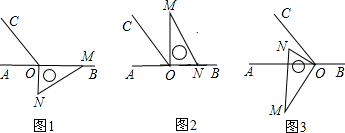
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
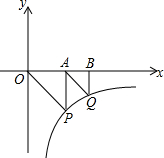 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )| A. | (6,0) | B. | (9,0) | C. | ($\frac{3+3\sqrt{5}}{2}$,0) | D. | ($\frac{3\sqrt{2}+3}{2}$,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com