练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某校举行春季运动会，需要在初三年级选取1或2名同学作为志愿者，初三（5）班的小熊、小乐和初三（6）班的小矛、小管4名同学报名参加．
    （1）若从这4名同学中随机选取1名志愿者，则被选中的这名同学恰好是初三（5）班同学的概率是；
    （2）若从这4名同学中随机选取2名志愿者，请用列举法（画树状图或列表）求这2名同学恰好都是初三（6）班同学的概率．

    【答案】
    （1）
    （2）解：列表如下：（小熊记作A，小乐记作B，小矛记作C，小管记作D），

    A

    B

    C

    D

    A

    ﹣﹣﹣﹣

    （B，A）

    （C，A）

    （D，A）

    B

    （A，B）

    ﹣﹣﹣﹣

    （C，B）

    （D，B）

    C

    （A，C）

    （B，C）

    ﹣﹣﹣﹣

    （D，C）

    D

    （A，D）

    （B，D）

    （C，D）

    ﹣﹣﹣﹣

    所有等可能的情况数有12种，其中这2名同学恰好都是初三（6）班同学的情况有2种，

    则P= =


    【解析】解：（1）若从这4名同学中随机选取1名志愿者，则被选中的这名同学恰好是初三（5）班同学的概率是 ； 故答案为： ；
    （1）四名同学中初三（5）班占一半，求出所求概率即可；（2）列表得出所有等可能的情况数，找出这2名同学恰好都是初三（6）班同学的情况数，即可求出所求概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点E（0，3），O（0，0），C（4，0）在⊙A上，BE是⊙A上的一条弦．则sin∠OBE= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点B，F，C，E在直线l上（F，C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC.

    （1）求证：△ABC≌△DEF；

    （2）指出图中所有平行的线段，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AD=BC,AB=CD,AD＞AB，将长方形ABCD折叠，使点C与点A重合，折痕为MN，连接CN．若△CDN的面积与△CMN的面积比为1：3，

    （1）求证：DN=BM；（2）求ND:NA的值；（3）求MN2：BM2的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连结CD．若点D与圆心O不重合，∠BAC=25°，则∠DCA的度数为度．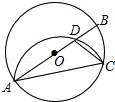

    查看答案和解析>>

    科目：初中数学 来源： 题型：

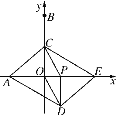
    【题目】如图，在平面直角坐标系中，点A，B的坐标分别是(－3，0)，(0，6)，动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP，CO为邻边构造PCOD.在线段OP延长线上一动点E，且满足PE＝AO.

    (1)当点C在线段OB上运动时，求证：四边形ADEC为平行四边形；

    (2)当点P运动的时间为秒时，求此时四边形ADEC的周长是多少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，甲、乙、丙三艘轮船从港口O出发，当分别行驶到A，B，C处时，经测量得，甲船位于港口的北偏东43°45′方向，乙船位于港口的北偏东76°35′方向，丙船位于港口的北偏西43°45′方向．

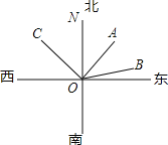
    （1）求∠BOC的度数；

    （2）求∠AOB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

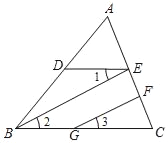
    【题目】已知：如图，BE∥GF，∠1＝∠3，∠DBC＝70°，求∠EDB的大小．

    阅读下面的解答过程，并填空(理由或数学式)

    解：∵BE∥GF(已知)

    ∴∠2＝∠3(　 　)

    ∵∠1＝∠3(　 　)

    ∴∠1＝(　 　)(　 　)

    ∴DE∥(　 　)(　 　)

    ∴∠EDB+∠DBC＝180°(　 　)

    ∴∠EDB＝180°﹣∠DBC(等式性质)

    ∵∠DBC＝(　 　)(已知)

    ∴∠EDB＝180°﹣70°＝110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】给下面命题的说理过程填写依据．

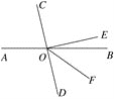
    已知：如图，直线AB，CD相交于点O，EO⊥CD，垂足为O，OF平分∠BOD，对∠EOF＝∠BOC说明理由．

    理由：因为∠AOC＝∠BOD( )，

    ∠BOF＝∠BOD( )，

    所以∠BOF＝∠AOC( )．

    因为∠AOC＝180°－∠BOC( )，

    所以∠BOF＝90°－∠BOC.

    因为EO⊥CD( )，

    所以∠COE＝90°( )

    因为∠BOE＋∠COE＝∠BOC( )，

    所以∠BOE＝∠BOC－∠COE.

    所以∠BOE＝∠BOC－90°( )

    因为∠EOF＝∠BOE＋∠BOF( )

    所以∠EOF＝(∠BOC－90°)＋(90°∠BOC)（ ）

    所以∠EOF＝∠BOC.

    查看答案和解析>>

    同步练习册答案