
【题目】给下面命题的说理过程填写依据.
已知:如图,直线AB,CD相交于点O,EO⊥CD,垂足为O,OF平分∠BOD,对∠EOF=![]() ∠BOC说明理由.
∠BOC说明理由.
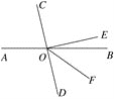
理由:因为∠AOC=∠BOD( ),
∠BOF=![]() ∠BOD( ),
∠BOD( ),
所以∠BOF=![]() ∠AOC( ).
∠AOC( ).
因为∠AOC=180°-∠BOC( ),
所以∠BOF=90°-![]() ∠BOC.
∠BOC.
因为EO⊥CD( ),
所以∠COE=90°( )
因为∠BOE+∠COE=∠BOC( ),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°( )
因为∠EOF=∠BOE+∠BOF( )
所以∠EOF=(∠BOC-90°)+(90°![]() ∠BOC)( )
∠BOC)( )
所以∠EOF=![]() ∠BOC.
∠BOC.
【答案】对顶角相等,角平分线的定义,等量代换,平角的定义,已知,垂直的定义,两角和的定义,等量代换,两角和的定义,等量代换.
【解析】
根据对顶角的性质得到∠AOC=∠BOD,由角平分线的定义得到∠BOF=![]() ∠BOD,等量代换得到∠BOF=
∠BOD,等量代换得到∠BOF=![]() ∠AOC,由垂直的定义得到∠COE=90°,等量代换得到∠BOE=∠BOC-90°,于是得到结论.
∠AOC,由垂直的定义得到∠COE=90°,等量代换得到∠BOE=∠BOC-90°,于是得到结论.
解:因为∠AOC=∠BOD(对顶角相等),∠BOF=![]() ∠BOD(平分线的定义),
∠BOD(平分线的定义),
所以∠BOF=![]() ∠AOC(等量代换).
∠AOC(等量代换).
因为∠AOC=180°-∠BOC(平角的定义),所以∠BOF=90°-![]() ∠BOC.
∠BOC.
因为EO⊥CD(已知),所以∠COE=90°(垂直的定义)
因为∠BOE+∠COE=∠BOC(两角和的定义),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°(等量代换)
因为∠EOF=∠BOE+∠BOF(两角和的定义)
所以∠EOF=(∠BOC-90°)+(90°![]() ∠BOC)(等量代换)
∠BOC)(等量代换)
所以∠EOF=![]() ∠BOC.
∠BOC.
故答案为:对顶角相等,角平分线的定义,等量代换,平角的定义,已知,垂直的定义,两角和的定义,等量代换,两角和的定义,等量代换.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校举行春季运动会,需要在初三年级选取1或2名同学作为志愿者,初三(5)班的小熊、小乐和初三(6)班的小矛、小管4名同学报名参加.
(1)若从这4名同学中随机选取1名志愿者,则被选中的这名同学恰好是初三(5)班同学的概率是;
(2)若从这4名同学中随机选取2名志愿者,请用列举法(画树状图或列表)求这2名同学恰好都是初三(6)班同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索
知识累计
解方程组![]()
解:设a﹣1=x,b+2=y,原方程组可变为![]()
解方程组得:![]() 即
即![]() 所以
所以![]() 此种解方程组的方法叫换元法.
此种解方程组的方法叫换元法.
(1)拓展提高
运用上述方法解下列方程组:
(2)能力运用
已知关于x,y的方程组![]() 的解为
的解为![]() ,直接写出关于m、n的方程组
,直接写出关于m、n的方程组![]() 的解为_____________.
的解为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(﹣3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.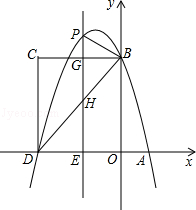
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,将矩形ABCD绕点C顺时针旋转90°,点B、D分别落在点B′,D′处,且点A,B′,D′在同一直线上,则tan∠DAD′ . 
查看答案和解析>>
科目:初中数学 来源: 题型:
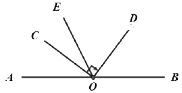
【题目】已知点A、O、B在一条直线上,将射线OC绕O点顺时针方向旋转90°后,得到射线OD,在旋转过程中,射线OC始终在直线AB上方,且OE平分∠AOD.约定,无论∠AOD大小如何,OE都看作是由OA、OD两边形成的最小角的平分线.
(1)如图,当∠AOC=30°时,∠BOD=_________°;
(2)若射线OF平分∠BOC,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上从左到右的三个点A,B,C所对应数的分别为a,b,c.其中点A、点B两点间的距离AB的长是2019,点B、点C两点间的距离BC的长是1000,
![]()
(1)若以点C为原点,直接写出点A,B所对应的数;
(2)若原点O在A,B两点之间,求|a|+|b|+|b﹣c|的值;
(3)若O是原点,且OB=19,求a+b﹣c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
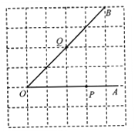
【题目】如图,点P,Q分别是∠AOB的边OA,OB上的点.
(1)过点P画OB的垂线,垂足为H;
(2)过点Q画OA的垂线,交OA于点C,连接PQ;
(3)线段QC的长度是点Q到 的距离, 的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是 (用“<”号连接).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com