
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.南方某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调査,毎人必选一种且只能选一种口味,并将调査情况绘制成如下两幅统计图(尚不完整):
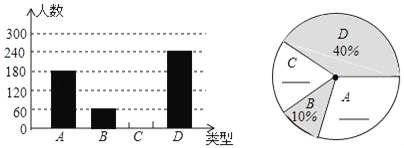
请根据以上信息冋答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)求扇形统计图中C所对圆心角的度数.
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】(10分)已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在距树![]() 米的地面上平放一面镜子
米的地面上平放一面镜子![]() ,人退后到距镜子
,人退后到距镜子![]() 米的
米的![]() 处,在镜子里恰巧看见树顶,若人眼
处,在镜子里恰巧看见树顶,若人眼![]() 距地面
距地面![]() 米.
米.

![]() 求树高;
求树高;
![]() 和
和![]() 是位似图形吗?若是,请指出位似中心;若不是,请说明理由.
是位似图形吗?若是,请指出位似中心;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A组数据为2、3、6、6、7、8、8、8,B组数据为4、5、8、8、9、10、10、10,则描述A、B两组数据的统计量中相等的是( )
A. 众数 B. 中位数 C. 平均数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+
x+![]() 与x轴、y轴分别交于点B、A,与直线y=
与x轴、y轴分别交于点B、A,与直线y=![]() 相交于点C.动点P从O出发在x轴上以每秒5个单位长度的速度向B匀速运动,点Q从C出发在OC上以每秒4个单位长度的速度,向O匀速运动,运动时间为t秒(0<t<2).
相交于点C.动点P从O出发在x轴上以每秒5个单位长度的速度向B匀速运动,点Q从C出发在OC上以每秒4个单位长度的速度,向O匀速运动,运动时间为t秒(0<t<2).
(1)直接写出点C坐标及OC、BC长;
(2)连接PQ,若△OPQ与△OBC相似,求t的值;
(3)连接CP、BQ,若CP⊥BQ,直接写出点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 可看成是分别以
可看成是分别以![]() 、
、![]() 、
、![]() 、
、![]() 为位似中心将正方形
为位似中心将正方形![]() 放大一倍得到的图形(正方形
放大一倍得到的图形(正方形![]() 的边长放大到原来的
的边长放大到原来的![]() 倍),由正方形
倍),由正方形![]() 到正方形
到正方形![]() ,我们称之作了一次变换,再将正方形
,我们称之作了一次变换,再将正方形![]() 作一次变换就得到正方形
作一次变换就得到正方形![]() ,…,依此下去,作了
,…,依此下去,作了![]() 次变换后得到正方形
次变换后得到正方形![]() ,若正方形
,若正方形![]() 的面积是
的面积是![]() ,那么正方形
,那么正方形![]() 的面积是多少( )
的面积是多少( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.
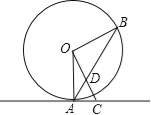
(1)AC与CD相等吗?为什么?
(2)若AC=2,AO=![]() ,求OD的长度.
,求OD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com