
【题目】如图所示,在距树![]() 米的地面上平放一面镜子
米的地面上平放一面镜子![]() ,人退后到距镜子
,人退后到距镜子![]() 米的
米的![]() 处,在镜子里恰巧看见树顶,若人眼
处,在镜子里恰巧看见树顶,若人眼![]() 距地面
距地面![]() 米.
米.

![]() 求树高;
求树高;
![]() 和
和![]() 是位似图形吗?若是,请指出位似中心;若不是,请说明理由.
是位似图形吗?若是,请指出位似中心;若不是,请说明理由.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】(8分)为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.

(1)从图象中可看出:印刷超过500页部分每页收费 元;
(2)现在乙印刷厂表示:每页0.15元收费.另收200元的制版费,乙印刷厂收费y(元)与印刷页数x(页)的函数关系为 ;
(3)在给出的坐标系内画出(2)中的函数图象,并结合函数图象回答印刷页数在3000页左右应选择哪个印刷店?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形的网格中,若点A的坐标为(﹣1,1),点B的坐标为(﹣2,0).

按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,直接写出点C的坐标 ( , );
(3)作出三角形ABC关于y轴对称的三角形A1B1C1;
(4)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,“任意三角形都是自相似图形”,只要顺次连接三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把![]() (图乙)第一次顺次连接各边中点所进行的分割,称为
(图乙)第一次顺次连接各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() );把
);把![]() 阶分割得出的
阶分割得出的![]() 个三角形再分别顺次连接它的各边中点所进行的分割,称为
个三角形再分别顺次连接它的各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() )…,依此规则操作下去.
)…,依此规则操作下去.![]() 阶分割后得到的每一个小三角形都是全等三角形(
阶分割后得到的每一个小三角形都是全等三角形(![]() 为正整数),设此时小三角形的面积为
为正整数),设此时小三角形的面积为![]() .请写出一个反映
.请写出一个反映![]() ,
,![]() ,
,![]() 之间关系的等式________.
之间关系的等式________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,“任意三角形都是自相似图形”,只要顺次连接三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把![]() (图乙)第一次顺次连接各边中点所进行的分割,称为
(图乙)第一次顺次连接各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() );把
);把![]() 阶分割得出的
阶分割得出的![]() 个三角形再分别顺次连接它的各边中点所进行的分割,称为
个三角形再分别顺次连接它的各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() )…,依此规则操作下去.
)…,依此规则操作下去.![]() 阶分割后得到的每一个小三角形都是全等三角形(
阶分割后得到的每一个小三角形都是全等三角形(![]() 为正整数),设此时小三角形的面积为
为正整数),设此时小三角形的面积为![]() .请写出一个反映
.请写出一个反映![]() ,
,![]() ,
,![]() 之间关系的等式________.
之间关系的等式________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 个单位长度的小正方形组成的网格中,给出了格点
个单位长度的小正方形组成的网格中,给出了格点![]() 和
和![]() (顶点是网格线的交点).点
(顶点是网格线的交点).点![]() 、
、![]() 坐标为
坐标为![]() ,
,![]() .
.
![]() 观察图形填空:
观察图形填空:![]() 是由
是由![]() 绕________点顺时针旋转________度得到的;
绕________点顺时针旋转________度得到的;
![]() 把
把![]() 中的图形作为一个新的”基本图形“,将新的基本图形绕
中的图形作为一个新的”基本图形“,将新的基本图形绕![]() 点顺时针旋转
点顺时针旋转![]() 度,请作出旋转后的图形,其中,
度,请作出旋转后的图形,其中,![]() 、
、![]() 、
、![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() 、
、![]() 、
、![]() .依次连接
.依次连接![]() 、
、![]() 、
、![]() 、
、![]() ,则四边形
,则四边形![]() 的形状为________;
的形状为________;
![]() 以
以![]() 点为位似中心,位似比为
点为位似中心,位似比为![]() (原图与新图对应边的比为
(原图与新图对应边的比为![]() ),作出四边形
),作出四边形![]() 的位似图形.
的位似图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.南方某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调査,毎人必选一种且只能选一种口味,并将调査情况绘制成如下两幅统计图(尚不完整):
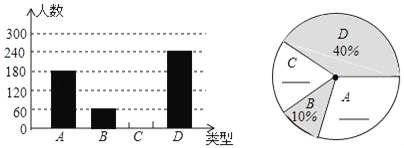
请根据以上信息冋答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)求扇形统计图中C所对圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC,其中正确的是: ___________(只需填写序号)。
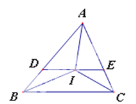
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.

(1)求∠F的度数;
(2)若CE=4,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com