
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.

(1)求∠F的度数;
(2)若CE=4,求DF的长.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在距树![]() 米的地面上平放一面镜子
米的地面上平放一面镜子![]() ,人退后到距镜子
,人退后到距镜子![]() 米的
米的![]() 处,在镜子里恰巧看见树顶,若人眼
处,在镜子里恰巧看见树顶,若人眼![]() 距地面
距地面![]() 米.
米.

![]() 求树高;
求树高;
![]() 和
和![]() 是位似图形吗?若是,请指出位似中心;若不是,请说明理由.
是位似图形吗?若是,请指出位似中心;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.
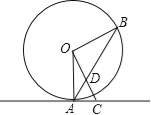
(1)AC与CD相等吗?为什么?
(2)若AC=2,AO=![]() ,求OD的长度.
,求OD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用![]() 个相同的小长方形与
个相同的小长方形与![]() 个小正方形镶嵌而成的正方形图案,已知该图案的面积为
个小正方形镶嵌而成的正方形图案,已知该图案的面积为![]() ,小正方形的面积为
,小正方形的面积为![]() ,若用
,若用![]() 表示小长方形的两边长(
表示小长方形的两边长(![]() ) ,请观察图案,指出以下关系式中,不正确的是( )
) ,请观察图案,指出以下关系式中,不正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC.点D从点B出发沿射线BC移动,以AD为边在AB的右侧作△ADE,且∠DAE=90°,AD=AE.连接CE.
(1)如图1,若点D在BC边上,则∠BCE=______度;
(2)如图2,若点D在BC的延长线上运动.
①∠BCE的度数是否发生变化?请说明理由;
②若BC=6,CD=2,求△ADE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积B.最大正方形的面积
C.较小两个正方形重叠部分的面积D.最大正方形与直角三角形的面积和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com