
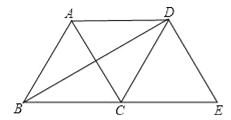
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【答案】D.
【解析】试题分析:根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD. ∵将等边△ABC绕点C顺时针旋转120°得到△EDC, ∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE, ∴∠ACD=120°﹣60°=60°, ∴△ACD是等边三角形,
∴AC=AD,AC=AD=DE=CE, ∴四边形ACED是菱形,
∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD, ∴AB=BC=CD=AD,
∴四边形ABCD是菱形, ∴BD⊥AC,∴①②③都正确


科目:初中数学 来源: 题型:
【题目】最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
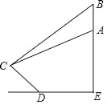
A. 91.1 B. 91.3 C. 58.2 D. 58.4
查看答案和解析>>
科目:初中数学 来源: 题型:
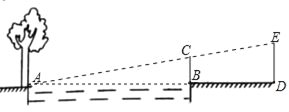
【题目】如图,洋洋和华华用所学的数学知识测量一条小河的宽度,河的对岸有一棵大树,底部记为点A,在他们所在的岸边选择了点B,并且使AB与河岸垂直,在B处与地面垂直竖起标杆BC,再在AB的延长线上选择点D,与地面垂直竖起标杆DE,使得A、C、E三点共线.经测量,BC=1m,DE=1.5m,BD=5m,求小河的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
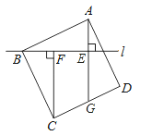
【题目】如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
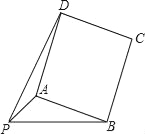
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
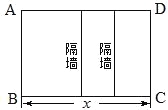
【题目】某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
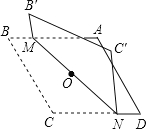
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
(1)方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为_____.
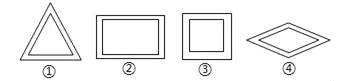
(2)如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应平行,且对应边之间的距离都相等,那么两个图形不相似的一组是(请填写正确答案的序号)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com