
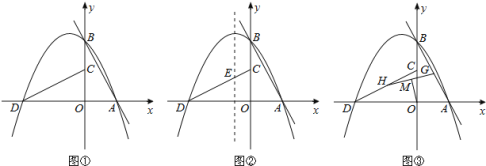
ЁОЬтФПЁПШчЭМЂйЃЌжБЯпLЃКy=mx+n(m<0ЃЌn>0)гыxЃЌyжсЗжБ№ЯрНЛгкAЃЌBСНЕуЃЌНЋЁїAOBШЦЕуOФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїCODЃЌЙ§ЕуAЃЌBЃЌDЕФХзЮяЯпPНазіLЕФЙиСЊХзЮяЯпЃЌЖјLНазіPЕФЙиСЊжБЯпЃЎ
(1)ШєLЃКy=-x+2ЃЌдђPБэЪОЕФКЏЪ§НтЮіЪНЮЊ______ЃЛШєPЃК![]() ЃЌдђ
ЃЌдђ![]() БэЪОЕФКЏЪ§НтЮіЪНЮЊ_______ЃЎ
БэЪОЕФКЏЪ§НтЮіЪНЮЊ_______ЃЎ
(2)ШчЭМЂкЃЌШєLЃКy=-3x+3ЃЌPЕФЖдГЦжсгыCDЯрНЛгкЕуEЃЌЕуFдкLЩЯЃЌЕуQдкPЕФЖдГЦжсЩЯЃЎЕБвдЕуCЃЌEЃЌQЃЌFЮЊЖЅЕуЕФЫФБпаЮЪЧвдCEЮЊвЛБпЕФЦНааЫФБпаЮЪБЃЌЧѓЕуQЕФзјБъЃЛ
(3)ШчЭМЂлЃЌШєLЃКy=mx+1ЃЌGЮЊABжаЕуЃЌHЮЊCDжаЕуЃЌСЌНгGHЃЌMЮЊGHжаЕуЃЌСЌНгOMЃЎШєOM=![]() ЃЌЧѓГіLЃЌPБэЪОЕФКЏЪ§НтЮіЪНЃЎ
ЃЌЧѓГіLЃЌPБэЪОЕФКЏЪ§НтЮіЪНЃЎ
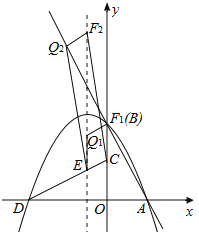
ЁОД№АИЁП(1)![]() ЃЛy=Љ2x+4ЃЛ(2)QзјБъЮЊQ1(Љ1ЃЌ
ЃЛy=Љ2x+4ЃЛ(2)QзјБъЮЊQ1(Љ1ЃЌ![]() )ЁЂQ2(Љ1ЃЌ
)ЁЂQ2(Љ1ЃЌ![]() )ЃЛ(3)y=Љ3x+1ЃЛy=Љ3x2Љ2x+1ЃЎ
)ЃЛ(3)y=Љ3x+1ЃЛy=Љ3x2Љ2x+1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШєlЃКy=-x+2ЃЌЧѓГіЕуAЁЂBЁЂDЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіPБэЪОЕФКЏЪ§НтЮіЪНЃЛШєPЃК![]() ЃЌЧѓГіЕуDЁЂAЁЂBЕФзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіlБэЪОЕФКЏЪ§НтЮіЪНЃЛ
ЃЌЧѓГіЕуDЁЂAЁЂBЕФзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіlБэЪОЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЖдГЦжсЕФЖЈвхНтД№МДПЩЃЛ
ЃЈ3ЃЉвдЕуCЃЌEЃЌQЃЌFЮЊЖЅЕуЕФЫФБпаЮЪЧвдCEЮЊвЛБпЕФЦНааЫФБпаЮЪБЃЌдђгаFQЁЮCEЃЌЧвFQ=CEЃЎвдДЫЮЊЛљДЁЃЌСаЗНГЬЧѓГіЕуQЕФзјБъЃЎзЂвтЃКЕуQЕФзјБъгаСНИіЃЌШчД№ЭМЫљЪОЃЌВЛвЊТЉНтЃЛ
ЃЈ4ЃЉШчД№ЭМЫљЪОЃЌзїИЈжњЯпЃЌЙЙдьЕШбќжБНЧШ§НЧаЮOGHЃЌЧѓГіOGЕФГЄЖШЃЌНјЖјгЩAB=2OGЧѓГіABЕФГЄЖШЃЌдйРћгУЙДЙЩЖЈРэЧѓГіy=mx+1жаmЕФжЕЃЌзюКѓЗжБ№ЧѓГіlЃЌPБэЪОЕФКЏЪ§НтЮіЪНЃЎ
НтЃК(1)![]() ЃЛy=Љ2x+4ЃЎ
ЃЛy=Љ2x+4ЃЎ
(2)Шє![]() ЃКy=Љ3x+3ЃЌдђA(1ЃЌ0)ЁЂB(0ЃЌ3)ЃЌ
ЃКy=Љ3x+3ЃЌдђA(1ЃЌ0)ЁЂB(0ЃЌ3)ЃЌ
ЁрC(0ЃЌ1)ЁЂD(Љ3ЃЌ0)ЃЎЧѓЕУжБЯпCDЕФНтЮіЪНЮЊЃКy=![]() x+1ЃЎПЩЧѓЕУ
x+1ЃЎПЩЧѓЕУ![]() ЕФЖдГЦжсЮЊx=Љ1ЃЎ
ЕФЖдГЦжсЮЊx=Љ1ЃЎ
ЁпвдЕуCЃЌEЃЌQЃЌFЮЊЖЅЕуЕФЫФБпаЮЪЧвдCEЮЊвЛБпЕФЦНааЫФБпаЮЃЌ
ЁрFQЁЮCEЃЌЧвFQ=CEЃЎ
ЩшжБЯпFQЕФНтЮіЪНЮЊЃКy=![]() x+bЃЎЁпЕуEЁЂЕуCЕФКсзјБъЯрВю1ЃЌ
x+bЃЎЁпЕуEЁЂЕуCЕФКсзјБъЯрВю1ЃЌ
ЁрЕуFЁЂЕуQЕФКсзјБъвВЪЧЯрВю1ЃЎдђ|xFЉ(Љ1)|=|xF+1|=1ЃЌНтЕУxF=0ЛђxF=Љ2ЃЎ
ЁпЕуFдкжБЯп![]() ЃКy=Љ2x+4ЩЯЃЌ
ЃКy=Љ2x+4ЩЯЃЌ
ЁрЕуFзјБъЮЊ(0ЃЌ3)Лђ(Љ2ЃЌ9)ЃЎ
ШєF(0ЃЌ3)ЃЌдђжБЯпFQЮЊЃКy=![]() x+3ЃЌ
x+3ЃЌ
ЕБx=Љ1ЪБЃЌy=![]() ЃЌЁрQ1(Љ1ЃЌ
ЃЌЁрQ1(Љ1ЃЌ![]() ).
).
ШєF(Љ2ЃЌ9)ЃЌдђжБЯпFQЮЊЃК![]() ЃЌ
ЃЌ
ЕБx=Љ1ЪБЃЌy= ![]() ЃЌЁрQ2(Љ1ЃЌ
ЃЌЁрQ2(Љ1ЃЌ![]() )ЃЎ
)ЃЎ
ЁрТњзуЬѕМўЕФЕуQга2ИіЃЌШчД№ЭМ1ЫљЪОЃЌЕуQзјБъЮЊQ1(Љ1ЃЌ![]() )ЁЂQ2(Љ1ЃЌ
)ЁЂQ2(Љ1ЃЌ![]() )ЃЎ
)ЃЎ
(3)ШчЭМ2ЫљЪОЃЌСЌНгOGЁЂOHЃЎЁпЕуGЁЂHЮЊаББпжаЕуЃЌ
ЁрOG=![]() ABЃЌOH=
ABЃЌOH=![]() CDЃЎ
CDЃЎ
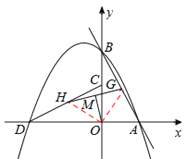
гЩа§зЊаджЪПЩжЊЃЌAB=CDЃЌOGЁЭOHЃЌ
ЁрЁїOGHЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЁпЕуGЮЊGHжаЕуЃЌ
ЁрЁїOMGЮЊЕШбќжБНЧШ§НЧаЮ.
ЁрOG=![]() OM=
OM=![]()
![]() =
=![]() .
.
ЁрAB=2OG=![]() ЃЎ
ЃЎ
Ёп![]() ЃКy=mx+1ЃЌ
ЃКy=mx+1ЃЌ
ЁрA(![]() ЃЌ0)ЃЌB(0ЃЌ1)ЃЎ
ЃЌ0)ЃЌB(0ЃЌ1)ЃЎ
дкRtЁїAOBжаЃЌгЩЙДЙЩЖЈРэЕУЃКOA2+OB2=AB2ЃЌМДЃК(![]() )2+12=(
)2+12=(![]() )2ЃЌ
)2ЃЌ
НтЕУЃКm=Љ3Лђm=3.
ЁпЕуBдкyжсе§АыжсЃЌ
Ёрm=3ЩсШЅЃЌ
Ёрm=Љ3ЃЎ
Ёр![]() БэЪОЕФКЏЪ§НтЮіЪНЮЊЃКy=Љ3x+1ЃЛ
БэЪОЕФКЏЪ§НтЮіЪНЮЊЃКy=Љ3x+1ЃЛ
ЁрB(0ЃЌ1)ЃЌD(Љ1ЃЌ0)ЃЎгжA(![]() ЃЌ0)ЃЌ
ЃЌ0)ЃЌ
РћгУД§ЖЈЯЕЪ§ЗЈЧѓЕУ![]() ЃКy=Љ3x2Љ2x+1ЃЎ
ЃКy=Љ3x2Љ2x+1ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
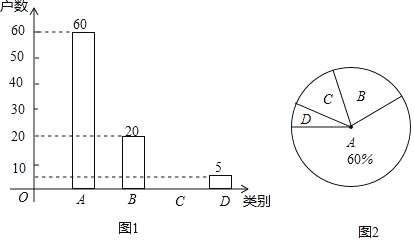
ЁОЬтФПЁПШчЭМЃЌаЁУїЯыВтСПаБЦТ![]() ХдвЛПУДЙжБгкЕиУц
ХдвЛПУДЙжБгкЕиУц![]() ЕФЪї
ЕФЪї![]() ЕФИпЖШЃЌЫћУЧЯШдкЕу
ЕФИпЖШЃЌЫћУЧЯШдкЕу![]() ДІВтЕУЪїЖЅ
ДІВтЕУЪїЖЅ![]() ЕФбіНЧЮЊ
ЕФбіНЧЮЊ![]() ЃЌШЛКѓдкЦТЖЅ
ЃЌШЛКѓдкЦТЖЅ![]() ВтЕУЪїЖЅ
ВтЕУЪїЖЅ![]() ЕФбіНЧЮЊ
ЕФбіНЧЮЊ![]() ЃЌвбжЊаБЦТ
ЃЌвбжЊаБЦТ![]() ЕФГЄЖШЮЊ
ЕФГЄЖШЮЊ![]() ЃЌаБЦТЖЅЕу
ЃЌаБЦТЖЅЕу![]() ЕНЕиУцЕФДЙжБИпЖШ
ЕНЕиУцЕФДЙжБИпЖШ![]() ЃЌдђЪї
ЃЌдђЪї![]() ЕФИпЖШЪЧЃЈ ЃЉ
ЕФИпЖШЪЧЃЈ ЃЉ![]()
A. 20![]() B. 30
B. 30![]() C. 30D. 40
C. 30D. 40
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOAЁЭOBЃЌABЁЭxжсгкЕуCЃЌЕуAЃЈ![]() ЃЌ1ЃЉдкЗДБШР§КЏЪ§
ЃЌ1ЃЉдкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЎ
ЕФЭМЯѓЩЯЃЎ

ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкxжсЕФИКАыжсЩЯДцдквЛЕуPЃЌЪЙЕУSЁїAOP=![]() SЁїAOBЃЌЧѓЕуPЕФзјБъЃЛ
SЁїAOBЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєНЋЁїBOAШЦЕуBАДФцЪБеыЗНЯђа§зЊ60ЁуЕУЕНЁїBDEЃЎжБНгаДГіЕуEЕФзјБъЃЌВЂХаЖЯЕуEЪЧЗёдкИУЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙњМвЮЊСЫЪЕЯж2020ФъШЋУцЭбЦЖФПБъЃЌЪЕЪЉЁАОЋзМЗіЦЖЁБеНТдЃЌВЩШЁвьЕиАсЧЈЃЌВњвЕЗіГжЕШДыЪЉЃЎЪЙЦЖРЇЛЇЕФЩњЛюЬѕМўЕУЕНИФЩЦЃЌЩњЛюжЪСПУїЯдЬсИпЃЎФГЦьЯиЮЊСЫШЋУцСЫНтЦЖРЇЯиЖдЗіЦЖЙЄзїЕФТњвтЖШЧщПіЃЌНјааЫцЛњГщбљЕїВщЃЌЗжЮЊЫФИіРрБ№ЃКAЃЎЗЧГЃТњвтЃЛBЃЎТњвтЃЛCЃЎЛљБОТњвтЃЛDЃЎВЛТњвтЃЎвРОнЕїВщЪ§ОнЛцжЦГЩЭМ1КЭЭМ2ЕФЭГМЦЭМЃЈВЛЭъећЃЉЃЎ
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉНЋЭМ1ВЙГфЭъећЃЛ
ЃЈ2ЃЉЭЈЙ§ЗжЮіЃЌЦЖРЇЛЇЖдЗіЦЖЙЄзїЕФТњвтЖШЃЈAЁЂBЁЂCРрЪгЮЊТњвтЃЉЪЧЁЁЁЁЃЛ
ЃЈ3ЃЉЪаЗіЦЖАьДгИУЦьЯиМзЯчеђ3ЛЇЁЂввЯчеђ2ЛЇЙВ5ЛЇЦЖРЇЛЇжаЃЌЫцЛњГщШЁСНЛЇНјааТњвтЖШЛиЗУЃЌЧѓетСНЛЇЦЖРЇЛЇЧЁКУЖМЪЧЭЌвЛЯчеђЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЦНУцжБНЧзјБъЯЕФкЕФЕуMТњзуКсЁЂзнзјБъЖМЮЊећЪ§ЃЌдђАбЕуMНазіЁАећЕуЁБЃЎР§ШчЃКPЃЈ1ЃЌ0ЃЉЁЂQЃЈ2ЃЌЉ2ЃЉЖМЪЧЁАећЕуЁБЃЎХзЮяЯпyЃНmx2Љ4mx+4mЉ2ЃЈmЃО0ЃЉгыxжсНЛгкЕуAЁЂBСНЕуЃЌШєИУХзЮяЯпдкAЁЂBжЎМфЕФВПЗжгыЯпЖЮABЫљЮЇГЩЕФЧјгђЃЈАќРЈБпНчЃЉЧЁгаЦпИіећЕуЃЌдђmЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A. ![]() ЁмmЃМ1B.
ЁмmЃМ1B. ![]() ЃМmЁм1C. 1ЃМmЁм2D. 1ЃМmЃМ2
ЃМmЁм1C. 1ЃМmЁм2D. 1ЃМmЃМ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
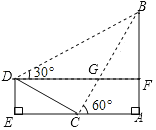
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯABC=90ЁуЃЌBA=BCЃЎЕуDЪЧABЕФжаЕуЃЌСЌНсCDЃЌЙ§ЕуBзїBGЁЭCDЃЌЗжБ№НЛCDЁЂCAгкЕуEЁЂFЃЌгыЙ§ЕуAЧвДЙжБгкABЕФжБЯпЯрНЛгкЕуGЃЌСЌНсDFЃЎИјГівдЯТЫФИіНсТлЃКЂй![]() ЃЛЂкЕуFЪЧGEЕФжаЕуЃЛЂлAF=
ЃЛЂкЕуFЪЧGEЕФжаЕуЃЛЂлAF=![]() ABЃЛЂмSЁїABC=5SЁїBDFЃЌЦфжае§ШЗЕФНсТлађКХЪЧЃЈЁЁЁЁЃЉ
ABЃЛЂмSЁїABC=5SЁїBDFЃЌЦфжае§ШЗЕФНсТлађКХЪЧЃЈЁЁЁЁЃЉ
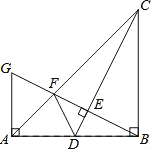
A. 4Иі B. 3Иі C. 2Иі D. 1Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнРюЗЩгыСѕССЩфЛїбЕСЗЕФГЩМЈЛцжЦСЫШчЭМЫљЪОЕФелЯпЭГМЦЭМЃЎ

ИљОнЭМЫљЬсЙЉЕФаХЯЂЃЌШєвЊЭЦМівЛЮЛГЩМЈНЯЮШЖЈЕФбЁЪжШЅВЮШќЃЌгІЭЦМіЃЈЁЁЁЁЃЉ
A. РюЗЩЛђСѕСС B. РюЗЩ C. СѕСС D. ЮоЗЈШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
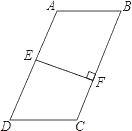
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌABЁЮDCЃЌEЪЧADжаЕуЃЌEFЁЭBCгкЕуFЃЌBC=5ЃЌEF=3ЃЎ
ЃЈ1ЃЉШєAB=DCЃЌдђЫФБпаЮABCDЕФУцЛ§S=__ЃЛ
ЃЈ2ЃЉШєABЃОDCЃЌдђДЫЪБЫФБпаЮABCDЕФУцЛ§SЁф__SЃЈгУЁАЃОЁБЛђЁА=ЁБЛђЁАЃМЁБЬюПеЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
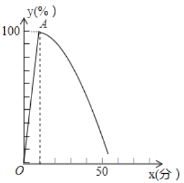
ЁОЬтФПЁПЛЊЮЊЭпЬиЪЕбщЪвЪдбщвЛжжаТаЭПьГфЕчГиЃЌГфЕчЪБЕчГиЕФЕчСП![]() ЪЧГфЕчЪБМф
ЪЧГфЕчЪБМф![]() ЃЈЗж
ЃЈЗж![]() ЕФвЛДЮКЏЪ§ЃЌЦфжа
ЕФвЛДЮКЏЪ§ЃЌЦфжа![]() ЃЎвбжЊГфЕчЧАЕчСПЮЊ
ЃЎвбжЊГфЕчЧАЕчСПЮЊ![]() ЃЌВтЕУГфЕч10ЗжжгКѓЕчСПДяЕН
ЃЌВтЕУГфЕч10ЗжжгКѓЕчСПДяЕН![]() ЃЌГфТњЕчКѓЪжЛњТэЩЯПЊЪМСЌајЙЄзїЃЌЙЄзїНзЖЮЕчГиЕчХЬ
ЃЌГфТњЕчКѓЪжЛњТэЩЯПЊЪМСЌајЙЄзїЃЌЙЄзїНзЖЮЕчГиЕчХЬ![]() ЪЧЙЄзїЪБМф
ЪЧЙЄзїЪБМф![]() ЕФЖўДЮКЏЪ§ЃЌШчЭМЫљЪОЃЌ
ЕФЖўДЮКЏЪ§ЃЌШчЭМЫљЪОЃЌ![]() ЪЧИУЖўДЮКЏЪ§ЖЅЕуЃЌгжВтЕУГфТњЕчКѓСЌајЙЄзїСЫ40ЗжжгЃЌетЪБЕчСПНЕЮЊ
ЪЧИУЖўДЮКЏЪ§ЖЅЕуЃЌгжВтЕУГфТњЕчКѓСЌајЙЄзїСЫ40ЗжжгЃЌетЪБЕчСПНЕЮЊ![]() ЃЌГЇЩЬЙцЖЈЪжЛњГфЕчЪБВЛФмЙЄзїЃЌЕчСПаЁгк
ЃЌГЇЩЬЙцЖЈЪжЛњГфЕчЪБВЛФмЙЄзїЃЌЕчСПаЁгк![]() ЪБЪжЛњВПЗжЙІФмНЋБЛЯожЦЃЌВЛФме§ГЃЙЄзїЃЎ
ЪБЪжЛњВПЗжЙІФмНЋБЛЯожЦЃЌВЛФме§ГЃЙЄзїЃЎ
ЃЈ1ЃЉЧѓГфЕчЪБКЭГфЕчКѓЪЙгУНзЖЮ![]() Йигк
Йигк![]() ЕФКЏЪ§БэДяЪНЃЈВЛгУаДГіШЁжЕЗЖЮЇЃЉЃЛ
ЕФКЏЪ§БэДяЪНЃЈВЛгУаДГіШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉЮЊЛёЕУИќЖрЪЕбщЪ§ОнЃЌЪЕбщЪвМЦЛЎдкЪзДЮГфТњЕчВЂЪЙгУ40ЗжжгКѓЭЃжЙЙЄзїдйДЮГфЕчЃЌГфЕч6ЗжжгКѓдйДЮЙЄзїЃЌМйЖЈЫљгаЕФЪЕбщЬѕМўВЛБфЧыЮЪЕкЖўДЮЙЄзїЕФЪБМфЖрГЄЃЈЕчСПЕН![]() ОЭЭЃжЙЙЄзїЃЉЃП
ОЭЭЃжЙЙЄзїЃЉЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com