
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() ≤m<1B.
≤m<1B. ![]() <m≤1C. 1<m≤2D. 1<m<2
<m≤1C. 1<m≤2D. 1<m<2
【答案】B
【解析】
画出图象,利用图象可得m的取值范围
∵y=mx2﹣4mx+4m﹣2=m(x﹣2)2﹣2且m>0,
∴该抛物线开口向上,顶点坐标为(2,﹣2),对称轴是直线x=2.
由此可知点(2,0)、点(2,﹣1)、顶点(2,﹣2)符合题意.
①当该抛物线经过点(1,﹣1)和(3,﹣1)时(如答案图1),这两个点符合题意.
将(1,﹣1)代入y=mx2﹣4mx+4m﹣2得到﹣1=m﹣4m+4m﹣2.解得m=1.
此时抛物线解析式为y=x2﹣4x+2.
由y=0得x2﹣4x+2=0.解得![]()
∴x轴上的点(1,0)、(2,0)、(3,0)符合题意.
则当m=1时,恰好有 (1,0)、(2,0)、(3,0)、(1,﹣1)、(3,﹣1)、(2,﹣1)、(2,﹣2)这7个整点符合题意.
∴m≤1.【注:m的值越大,抛物线的开口越小,m的值越小,抛物线的开口越大】
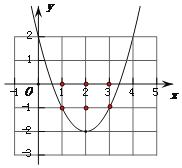
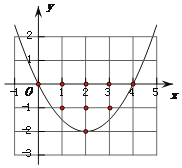
答案图1(m=1时) 答案图2( m=![]() 时)
时)
②当该抛物线经过点(0,0)和点(4,0)时(如答案图2),这两个点符合题意.
此时x轴上的点 (1,0)、(2,0)、(3,0)也符合题意.
将(0,0)代入y=mx2﹣4mx+4m﹣2得到0=0﹣4m+0﹣2.解得m=![]() .
.
此时抛物线解析式为y=![]() x2﹣2x.
x2﹣2x.
当x=1时,得![]() .∴点(1,﹣1)符合题意.
.∴点(1,﹣1)符合题意.
当x=3时,得![]() .∴点(3,﹣1)符合题意.
.∴点(3,﹣1)符合题意.
综上可知:当m=![]() 时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,﹣1)、(3,﹣1)、(2,﹣2)、(2,﹣1)都符合题意,共有9个整点符合题意,
时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,﹣1)、(3,﹣1)、(2,﹣2)、(2,﹣1)都符合题意,共有9个整点符合题意,
∴m=![]() 不符合题.
不符合题.
∴m>![]() .
.
故选:B.


科目:初中数学 来源: 题型:
【题目】某校初三一班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是_________分,乙队成绩的众数是_________分;
(2)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是_________队;
(3)测试结果中,乙队获满分的四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛,用树状图或列表法求恰好抽中一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D是CB延长线上一点,∠BAD=∠BAC.
(1)如图,求证:![]() ;
;
(2)如图,在AD上有一点E,∠EBA=∠ACB=120°.若AC=2BC=2,求DE的长;
(3)如图,若AB=AC=2BC=4,BE⊥AB交AD于点E,直接写出△BDE的面积.
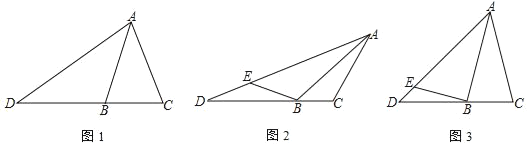
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设快车离乙地的距离为y1(km),慢车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为s(km).y1,y2与x的函数关系图象如图1所示,s与x的函数关系图象如图2所示.则下列判断:①图1中a=3;②当x=![]() h时,两车相遇;③当x=
h时,两车相遇;③当x=![]() 时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=
时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=![]() h或
h或![]() h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)
h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线L:y=mx+n(m<0,n>0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做L的关联抛物线,而L叫做P的关联直线.
(1)若L:y=-x+2,则P表示的函数解析式为______;若P:![]() ,则
,则![]() 表示的函数解析式为_______.
表示的函数解析式为_______.
(2)如图②,若L:y=-3x+3,P的对称轴与CD相交于点E,点F在L上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(3)如图③,若L:y=mx+1,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=![]() ,求出L,P表示的函数解析式.
,求出L,P表示的函数解析式.
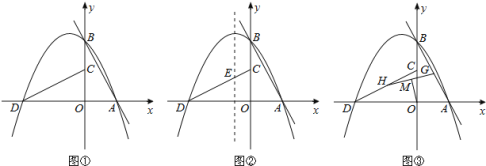
查看答案和解析>>
科目:初中数学 来源: 题型:
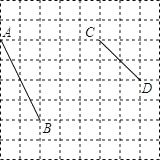
【题目】如图,在小正方形的边长均为1的方格纸中,有线段![]() 和线段
和线段![]() ,点
,点![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
(1)在方格纸中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点E在小正方形的顶点上,且
,点E在小正方形的顶点上,且![]() 的面积为5;
的面积为5;
(2)在方格纸中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在小正方形的顶点上,
在小正方形的顶点上,![]() 的面积为4,射线
的面积为4,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com