
 如图,将Rt△ABC绕直角顶点C按顺时针旋转90°到△DEC的位置,已知斜边AB=10cm,BC=6cm.设DE的中点为M,连接AM,则AM的长为( )
如图,将Rt△ABC绕直角顶点C按顺时针旋转90°到△DEC的位置,已知斜边AB=10cm,BC=6cm.设DE的中点为M,连接AM,则AM的长为( )| A. | 4 | B. | 5 | C. | 6 | D. | $\sqrt{41}$ |
分析 首先过点M作MF⊥EC于点F,结合旋转的性质进而结合三角形中位线的性质得出FM,AF的长,进而利用勾股定理得出AM的长.
解答 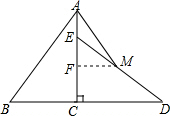 解:如图所示:过点M作MF⊥EC于点F,
解:如图所示:过点M作MF⊥EC于点F,
∵斜边AB=10cm,BC=6cm,
∴AC=8cm,
∵将Rt△ABC绕直角顶点C按顺时针旋转90°到△DEC的位置,
∴AC=CD=8cm,EC=BC=6cm,
∵DE的中点为M,MF⊥EC,
∴EF=FC=3cm,
∴FM=$\frac{1}{2}$DC=4cm,AF=5cm,
∴AM=$\sqrt{A{F}^{2}+F{M}^{2}}$=$\sqrt{{5}^{2}{+4}^{2}}$=$\sqrt{41}$(cm).
故选:D.
点评 此题主要考查了旋转的性质以及勾股定理和三角形中位线的性质等知识,正确得出AF的长是解题关键.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
| A. | a≠-2 | B. | a≠0 | C. | a≠2且a≠-2 | D. | a≠0或a≠-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{xy=1}\\{x+y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x-2y=1}\\{\frac{1}{x}+y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+z=0}\\{3x-y=\frac{1}{5}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+\frac{y}{2}=5}\\{\frac{x}{2}+\frac{y}{3}=7}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某油田有四个油井分别位于A,B,C,D四个点上,如果要建一个维修站H,使这个维修站到这四个油井的距离之和最短,那么这个维修站就必须建于AC,BD的交点上,知道这是为什么吗?
如图,某油田有四个油井分别位于A,B,C,D四个点上,如果要建一个维修站H,使这个维修站到这四个油井的距离之和最短,那么这个维修站就必须建于AC,BD的交点上,知道这是为什么吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三种都有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角△ACD中,B为AD延长线上一点,且满足AB=CD,在CD上的一点E满足DE=DB,连接BE,F为BE中点,延长AF与过B点的DC的平行线交于点G,连接CG,求证:∠CAG=45°,AD+BG=CG.
如图,直角△ACD中,B为AD延长线上一点,且满足AB=CD,在CD上的一点E满足DE=DB,连接BE,F为BE中点,延长AF与过B点的DC的平行线交于点G,连接CG,求证:∠CAG=45°,AD+BG=CG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2-7=(+2)+(-7) | B. | (-5)÷(-$\frac{1}{2}$)=-5×(-2) | C. | 7x-(x+1)=7x-x-1 | D. | 3(x+8)=3x+8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com