Question

14．已知直线l及位于其两侧的两点A，B，如图
（1）在图①中的直线l上求一点P，使PA=PB；
（2）在图②中的直线l上求一点Q，使直线l平分∠AQB；
（3）能否在直线l上找一点，使该点到点A，B的距离之差的绝对值最大？若能，直接指出该点的位置，若不能，请说明理由．

Answer 1

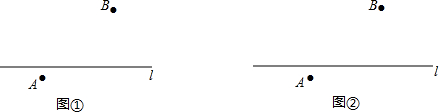
分析 （1）作线段AB的垂直平分线与l的交点即为所求．
（2）作点A关于l的对称点A′，连接BA′并延长交l于点Q，点Q即为所求．
（3）图2中的点Q即为所求．

解答 解：（1）连接AB作线段AB的垂直平分线MN，直线MN和直线l的交点为P，点P即为所求，见图①．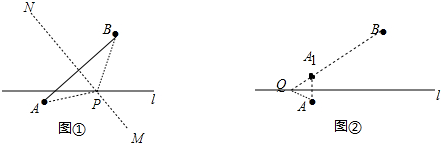
（2）作点A关于直线l的对称点A₁，连接BA₁且延长交直线l于点Q，点Q即为所求，见图②．
（3）图②中的点Q即为所求，见图③．
理由如下：在直线l上任意取一点Q₁，连接Q₁A₁，Q₁B，Q₁A，
∵A、A′关于直线l对称，
∴Q₁A₁=Q₁A，
∵|Q₁A₁-Q₁B|≤A₁B（当Q₁与Q重合时等号成立），
∴|Q₁A-Q₁B|≤A₁B，
∵Q₁与Q重合时，
|QB-QA₁|=A₁B，
故点Q即为所求的点．

点评 本题考查线段的垂直平分线性质、轴对称的性质以及三角形三边关系等知识，灵活运用这些知识是解题的关键．