
【题目】如图,已知楼房![]() 旁边有一池塘,池塘中有一电线杆
旁边有一池塘,池塘中有一电线杆![]() 高
高![]() 米,在池塘边
米,在池塘边![]() 处测得电线杆顶端
处测得电线杆顶端![]() 的仰角为
的仰角为![]() ,楼房顶点
,楼房顶点![]() 的仰角为
的仰角为![]() ,又在池塘对面的
,又在池塘对面的![]() 处,观测到
处,观测到![]() ,
,![]() ,
,![]() 在同一直线上时,测得电线杆顶端
在同一直线上时,测得电线杆顶端![]()
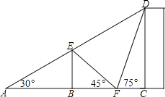
的仰角为![]() . (注:tan75
. (注:tan75![]() =2+
=2+![]() )
)
(1)求池塘边![]() ,
,![]() 两点之间的距离;
两点之间的距离;
(2)求楼房![]() 的高.
的高.
【答案】![]() 间的距离为
间的距离为![]() 米,楼房
米,楼房![]() 的高为
的高为![]() 米.
米.
【解析】
(1)分别解Rt△ABE与Rt△BEF,可得AB与BF的大小.由AF=AB+BF可得结果;
(2)设CD=x.在Rt△FCD中,可得CF的值,根据相似三角形的性质,可得比例关系求解.
解:如图:
(1)在Rt△ABE中,
![]() ∠A=30
∠A=30![]() ,BE=10,
,BE=10,
![]()
![]() =
=![]()
![]() AB=10
AB=10![]() ,
,
在Rt△EBF中,
![]() ∠BFE=45
∠BFE=45![]() ,
,
![]() BF=BE=10,
BF=BE=10,
![]() AF=10+10
AF=10+10![]() ;
;
(2)![]() BE=10,∠A=30
BE=10,∠A=30![]() ,
,![]() AB=10
AB=10![]() ,
,
设CD=x.则CF=![]() =
=![]() .
.
![]() ∠EBA=∠DCA=90
∠EBA=∠DCA=90![]() ,∠A=30
,∠A=30![]() ,
,
![]() △ABE~△ACD,
△ABE~△ACD,
由相似三角形的性质可得:![]() ,
,
即![]() ,
,
解得x=10+5![]() .
.
答:AF间的距离为(10+10![]() )米,楼房CD的高为(10+5
)米,楼房CD的高为(10+5![]() )米.
)米.


科目:初中数学 来源: 题型:
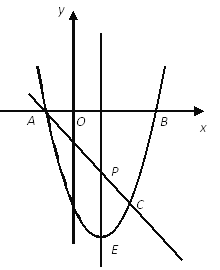
【题目】如图,抛物线![]() 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是![]() ,则点C的坐标是( )
,则点C的坐标是( )

A. (4,2) B. (2,4) C. (![]() ,3) D. (3,
,3) D. (3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某小船准备从![]() 处出发,沿北偏东
处出发,沿北偏东![]() 的方向航行,在规定的时间将一批物资运往
的方向航行,在规定的时间将一批物资运往![]() 处的货船上,后考虑这条航线可能会因退潮而使小船搁浅,决定改变航线,从
处的货船上,后考虑这条航线可能会因退潮而使小船搁浅,决定改变航线,从![]() 处出发沿正东方向航行
处出发沿正东方向航行![]() 海里到达
海里到达![]() 处,再由
处,再由![]() 处沿北偏东
处沿北偏东![]() 的方向航行到达
的方向航行到达![]() 处.
处.

(1)小船由![]() 经
经![]() 到达
到达![]() 走了多少海里(结果精确到
走了多少海里(结果精确到![]() 海里);
海里);
(2)为了按原定时间到达![]() 处的货船上,小船提速,每小时增加
处的货船上,小船提速,每小时增加![]() 海里,求小船原定的速度(结果精确到
海里,求小船原定的速度(结果精确到![]() 海里/时).
海里/时).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:
①若a≠b,则a2≠b2;②对于不为零的实数c,关于x的方程![]() 的根是c.
的根是c.
③对角线互相垂直平分的四边形是菱形.④过一点有且只有一条直线与已知直线平行.
⑤在反比例函数![]() 中,如果函数值y<1时,那么自变量x>2,是真命题的个数是 ( )
中,如果函数值y<1时,那么自变量x>2,是真命题的个数是 ( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com