
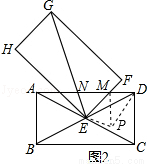
(10分)如图1,四边形ABCD、EFGH为全等的矩形.且矩形ABCD的对角线交于点E,点A在EG上,∠ACB=300.将矩形EFGH绕点E顺时针旋转а角(00<а<600),如图2,GE、FE与AD分别相交于N、M.
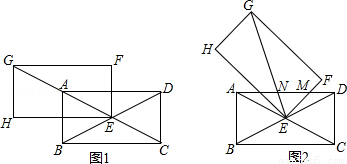
(1)求证:AN+DM>MN;
(2)若MN2+DM2=AN2,求旋转角а的大小.
(1)证明见试题解析;(2)45°.
【解析】
试题分析:(1)根据矩形的对角线互相平分且相等可得AE=DE,再求出∠AED=120°,将△AEN绕点E顺时针旋转120°得到△DPE,连接MP,根据旋转的性质可得EP=NE,DP=AN,∠DEP=∠EN,再求出∠MEN=∠MEP=60°,然后利用“边角边”证明△MEN和△MEP全等,根据全等三角形对应边相等可得MN=MP,然后利用三角形的任意两边之和大于第三边证明即可;
(2)利用勾股定理逆定理判断出△DPM是直角三角形,根据全等三角形对应角相等可得∠EMN=∠EMP=45°,利用三角形的内角和定理求出∠MNE=75°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEN=45°,即为旋转角度数.
试题解析:(1)∵四边形ABCD是矩形,∴AE=DE,
∵∠ACB=30°,∴∠AED=180°﹣30°×2=120°,
将△AEN绕点E顺时针旋转120°得到△DPE,连接MP,
则EP=NE,DP=AN,∠DEP=∠EN,
∵∠AED=120°,∴∠MEN=∠MEP=60°,
在△MEN和△MEP中,
∵EP=NE,∠MEN=∠MEP,EM=EM,∴△MEN≌△MEP(SAS),∴MN=MP,
由三角形的三边关系得,DP+DM>MP,∴AN+DM>MN;
(2)【解析】
∵MN2+DM2=AN2,∴△DPM是直角三角形,∠DMP=90°,
∵△MEN≌△MEP,∴∠EMN=∠EMP=45°,
在△MNE中,∠MNE=180°﹣45°﹣60°=75°,
在△ANE中,∠AEN=∠MNE﹣∠CAD=75°﹣30°=45°,
∴旋转角为45°.
考点:旋转的性质.
考点分析: 考点1:图形的平移与旋转 定义:

科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第一次摸底数学试卷(解析版) 题型:解答题
(10分)张明、王成两位同学初二一学年10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如下图所示:利用图中提供的信息,解答下列问题.
(1)完成下表
姓名 | 平均成绩 | 中位数 | 众数 | 方差(S2) |
张明 | 80 | 80 | ||
王成 | 260 |
(2)如果将90分以上(含90分)的成绩视为A等,则获得成绩为A等多的同学是 ;
(3)根据图表信息,请你对这位两同学各提一条不超过20个字的学习建议,并说明提出建议的原因.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省平顶山市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如果关于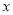 的一元二次方程
的一元二次方程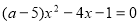 有实数根,则
有实数根,则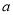 满足条件是( )
满足条件是( )
A、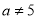 B、
B、 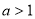 且
且 C、.
C、. 且
且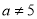 D、
D、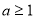
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南平顶山四十三中八年级上学期第一次段测数学试卷(解析版) 题型:填空题
某农舍的大门是一个木制的矩形栅栏,它的高为4m,宽为3m,现需要在相对的顶点间用一块木棒加固,木板的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com