Question

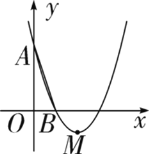
【题目】如图，在平面直角坐标系xOy中，已知抛物线y＝x2＋bx＋C经过A(0，3)，B(1，0)两点，顶点为M.

(1)求b、C的值；

(2)将△OAB绕点B顺时针旋转90°后，点A落到点C的位置，该抛物线沿y轴上下平移后经过点C，求平移后所得抛物线的表达式；

(3)设(2)中平移所得的抛物线与y轴的交点为A1，顶点为M1，若点P在平移后的抛物线上，且满足△PMM1的面积是△PAA1面积的3倍，求点P的坐标．

Answer 1

【答案】(1)b=-4,c=3;(2) y＝x2－4x＋1；(3) P (，－)或(－1，6)．

【解析】

（1）直接将已知点的坐标代入到二次函数的解析式中求得未知系数的值即可；
（2）根据A、B两点的坐标可以求得OA和OB的长，然后根据旋转的性质求得点C的坐标，然后向下平移2个单位即可得到平移后的抛物线的解析式；
（3）设P点的坐标为（x0，x02-4x0+1），然后分0＜x0＜2时和x0＜0时两种情况利用S△PMM1=3S△PAA1得到有关x0的方程求得x0即可确定点P的坐标即可．

解：(1)∵抛物线y＝x2＋bx＋C经过A(0，3)，B(1，0)两点，

∴，解得；

(2)由(1)知，抛物线的表达式为y＝x2－4x＋3.

∵A(0，3)，B(1，0)

∴OA＝3，OB＝1，

∴C点坐标为(4，1)，

当x＝4时，由y＝x2－4x＋3得y＝3，

则抛物线y＝x2－4x＋3经过点(4，3)，

∴将原抛物线沿y轴向下平移2个单位后过点C，

∴平移后的抛物线的表达式为y＝x2－4x＋1；

(3)∵点P在y＝x2－4x＋1上，可设P点的坐标为(x0，x02－4x0＋1)

将y＝x2－4x＋1配方得y＝(x－2)2－3，

∴抛物线的对称轴为直线x＝2，

∵S△PMM1＝|x0－2|·MM1，

S△PAA1＝ |x0|·AA1，

S△PMM1＝3S△PAA1，MM1＝AA1＝2，

∴x0<2，|x0－2|＝3|x0|.

分情况讨论：

①当0<x0<2时，

则有2－x0＝3x0，

解得x0＝，则x02－4x0＋1＝－，

∴点P的坐标为(，－)；

②当x0<0时，

则有2－x0＝－3x0，解得x0＝－1，则x02－4x0＋1＝6，

∴点P的坐标为(－1，6)．

故满足△PMM1的面积是△PAA1面积的3倍时，点P的坐标为(，－)或(－1，6)．