
分析 (1)根据比例的性质,可得线段AB、线段BC的长,根据线段的和差,可得线段AD的长,根据线段中点的性质,可得MD的长,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得AM的长,根据线段的和差,可得BM的长,根据比的意义,可得答案.
解答 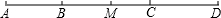 解:(1)由AB:BC:CD=2:4:3,CD=12cm,得
解:(1)由AB:BC:CD=2:4:3,CD=12cm,得
AB=8cm,BC=16cm.
由线段的和差,得
AD=AB+BC+CD=36cm.
由线段中点的性质,得
AM=MD=$\frac{1}{2}$AD=18cm.
由线段的和差,得
MC=MD-CD=18-12=6(cm);
(2)由线段的和差,得
BM=AM-AB=18-8=10(cm).
由比的意义,得
AB:BM=4:5.
点评 本题考查了两点间的距离.利用了线段的和差,线段中点的性质.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
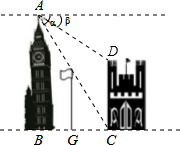 如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com