

���� ��1�����ݻ������DZ߳�Ϊa�ĵȱ�������������������жϼ��ɣ�
��2�����ݻ������DZ߳�Ϊa���Խ��߳�Ϊb���������ĸ���������жϼ��ɣ�
��3���������˶�����Ҫ��������������������ÿ�λ����ľ��붼���������n�λ�����ÿ����ȫ������һ�Σ��ۻ���n�κ����ص���1����A1��������2 �Ǵ��ģ�������ڢٸ�������
��4��������������ÿ�λ����ľ��붼���������n�λ�����ÿ����ȫ������һ�Σ��ۻ���n�κ����ص���1����A1�����м��㼴�ɵó�S4=3+2+1+2=8��S5=4+3+2+1+2=12��
��5�������n ���㣬��һ��Ҫ���ֻ���Ǵӵ�1 ���㵽��n ���㣬������n-1����2��Ҫ���ֻ���Ǵӵ�n ���㵽��2 ����������n-2�����մ˹��ɣ����n ������������
�����м�ĵ�$\frac{n+1}{2}$���˵�ص���1�������Ϊ$\frac{n+1}{2}-1$�����n Ϊż��������ĵ���$\frac{n}{2}+1$���˵�ص���1 �������Ϊ$\frac{n}{2}$���ݴ˽��м��㼴�ɣ�
���  �⣺��1����ͼ1���������DZ߳�Ϊa�ĵȱ��������������㣬
�⣺��1����ͼ1���������DZ߳�Ϊa�ĵȱ��������������㣬
��S3=3a��
�ʴ�Ϊ��3a��
��2����ͼ2���������DZ߳�Ϊa���Խ��߳�Ϊb���������ĸ����㣬
��S4=2a+2b��
�ʴ�Ϊ��2a+2b��
��3����ͼ4���١߷���2 �Ǵ��ģ�������ڢٸ�������ÿһ�ξ���Ҫ�����ģ�
���1��ȷ��
��ѡA��
����ͼ3��S3=2+1+1=4��
�ʴ�Ϊ��4��
��4��������������ÿ�λ����ľ��붼���������n�λ�����ÿ����ȫ������һ�Σ��ۻ���n�κ����ص���1����A1���ɵã�
S4=3+2+1+2=8��
S5=4+3+2+1+2=12��
�ʴ�Ϊ��8��12��
��5��n Ϊ����ʱ��Sn=n-1+n-2+��+1+$\frac{n+1}{2}$-1=$\frac{{n}^{2}-1}{2}$��
n Ϊż��ʱ��Sn=n-1+n-2+��+1+$\frac{n}{2}$=$\frac{{n}^{2}}{2}$��
���� ������Ҫ�������й������Σ������Լ��߶εı仯��Ĺ��������⣬�������Ĺؼ������⡰�����˶����������������ÿ�λ����ľ��붼���������n�λ�����ÿ����ȫ������һ�Σ�����n�κ����ص���1����A1�����Ǽ������Ҫ���ݣ�����ʱע�����˼������ã�


 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪Rt��ABC��Rt��ADE����ABC=��ADE=90�㣬BC��DE�ཻ�ڵ�F������ CD��EB��
��ͼ����֪Rt��ABC��Rt��ADE����ABC=��ADE=90�㣬BC��DE�ཻ�ڵ�F������ CD��EB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
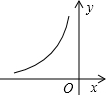 ��ͼ���Ƿ���������y=$\frac{1-m}{x}$��ͼ���е�һ֧����ش�
��ͼ���Ƿ���������y=$\frac{1-m}{x}$��ͼ���е�һ֧����ش��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ԲO�Ƶ�M��ת����O��ת����O�䣬������ԲO�Ƶ�M��ת��õ���ͼ�Σ�
��ͼ����ԲO�Ƶ�M��ת����O��ת����O�䣬������ԲO�Ƶ�M��ת��õ���ͼ�Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com