
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列四个结论中:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.正确的有( )
MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列四个结论中:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.正确的有( )
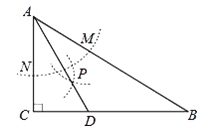
A.只有①②③B.只有①②④C.只有①③④D.①②③④
【答案】D
【解析】
由基本作图可知①正确;根据三角形内角和定理求出∠CAB的度数,再由AD是∠BAC的平分线得出∠1=∠2=30°,根据直角三角形的性质可判断②正确;根据∠1=∠B可得AD=BD,进而判断③正确;先根据直角三角形的性质得出AD=2CD,求出BC=3CD即可判断④正确.
解:①由基本作图可知AD是∠BAC的平分线,故①正确;
②∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°∠2=60°,即∠ADC=60°,故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上,故③正确;
④∵在Rt△ACD中,∠2=30°,
∴AD=2CD,
∵AD=BD,
∴BD=2CD,
∴BC=3CD,
∴S△DAC:S△ABC=1:3,故④正确;
故选:D.


科目:初中数学 来源: 题型:
【题目】为了丰富学生校园文化生活,促进学生学习兴趣和能力的提高,我校在初一年级开始设置选修课程,共设立课程12门,下图为其中的四门课程(包括趣味数学、篮球队、戏剧社、合唱团)的参加人数统计图:
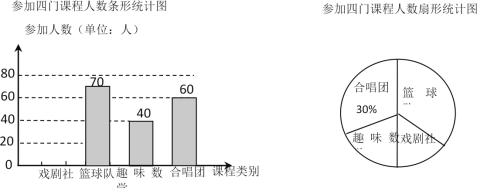
(1)学校初一年级参加这四门课程的总人数是 人;
(2)扇形统计图中“趣味数学”部分的圆心角是 度,并把条形统计图补充完整;
(3)学校原则上每一门课程组成一个班,但参加篮球队的学生实在太多,考虑场地因素则分成两个班,合唱团由于课程特征还是组成一个班,求这四门课程平均每班多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五水共治办公室在一次巡查时测量一排水管的排水情况,如图,水平放置的圆柱形排水管的截面为⊙O,半径是10cm,有水部分弓形的高为5cm,

(1)求AB的长;
(2)求截面中有水部分弓形的面积。(保留根号及π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求![]() 的值.
的值.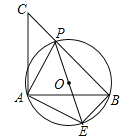
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,m),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
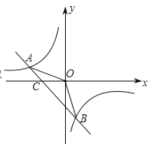
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
(3)根据图像直接写出使![]() 成立的x的取值范围
成立的x的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
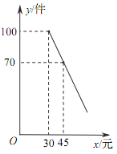
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).
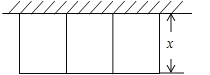
(1)求y关于x的函数表达式,并直接写出自变量x的取值范围;
(2)三间饲养室占地总面积有可能达到210m2吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
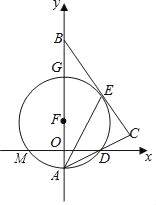
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,经过A,D两点的圆的圆心F恰好在y轴上,⊙F与边BC相切于点E,与x轴交于点M,与y轴相交于另一点G,连接AE.
(1)求证:AE平分∠BAC;
(2)若点A,D的坐标分别为(0,﹣1),(2,0),求⊙F的半径;
(3)求经过三点M,F,D的抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com