
ЁОЬтФПЁПдФЖСЯТУцЕФВФСЯЃК
НтЗНГЬx4Љ7x2+12=0етЪЧвЛИівЛдЊЫФДЮЗНГЬЃЌИљОнИУЗНГЬЕФЬиЕуЃЌЫќЕФНтЗЈЭЈГЃЪЧЃКЩшx2=yЃЌдђx4=y2ЃЌЁрдЗНГЬПЩЛЏЮЊЃКy2Љ7y+12=0ЃЌНтЕУy1=3ЃЌy2=4ЃЌЕБy=3ЪБЃЌx2=3ЃЌx=ЁР![]() ЃЌЕБy=4ЪБЃЌx2=4ЃЌx=ЁР2ЃЎЁрдЗНГЬгаЫФИіИљЪЧЃКx1=
ЃЌЕБy=4ЪБЃЌx2=4ЃЌx=ЁР2ЃЎЁрдЗНГЬгаЫФИіИљЪЧЃКx1=![]() ЃЌx2=Љ
ЃЌx2=Љ![]() ЃЌx3=2ЃЌx4=Љ2ЃЌвдЩЯЗНЗЈНаЛЛдЊЗЈЃЌДяЕНСЫНЕДЮЕФФПЕФЃЌЬхЯжСЫЪ§бЇЕФзЊЛЏЫМЯыЃЌдЫгУЩЯЪіЗНЗЈНтД№ЯТСаЮЪЬтЃЎ
ЃЌx3=2ЃЌx4=Љ2ЃЌвдЩЯЗНЗЈНаЛЛдЊЗЈЃЌДяЕНСЫНЕДЮЕФФПЕФЃЌЬхЯжСЫЪ§бЇЕФзЊЛЏЫМЯыЃЌдЫгУЩЯЪіЗНЗЈНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉНтЗНГЬЃКЃЈx2+xЃЉ2Љ5ЃЈx2+xЃЉ+4=0ЃЛ
ЃЈ2ЃЉвбжЊЪЕЪ§aЃЌbТњзуЃЈa2+b2ЃЉ2Љ3ЃЈa2+b2ЃЉЉ10=0ЃЌЪдЧѓa2+b2ЕФжЕЃЎ
ЁОД№АИЁПМћНтЮі
ЁОНтЮіЁПНтЃКЃЈ1ЃЉЩшy=x2+xЃЌдђy2Љ5y+4=0ЃЌ
ећРэЃЌЕУ
ЃЈyЉ1ЃЉЃЈyЉ4ЃЉ=0ЃЌ
НтЕУy1=1ЃЌy2=4ЃЌ
ЕБx2+x=1МДx2+xЉ1=0ЪБЃЌНтЕУЃКx=![]() ЃЛ
ЃЛ
ЕБЕБx2+x=4МДx2+xЉ4=0ЪБЃЌНтЕУЃКx=![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌдЗНГЬЕФНтЮЊx1ЃЌ2=![]() ЃЌx3ЃЌ4=
ЃЌx3ЃЌ4=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшx=a2+b2ЃЌдђx2Љ3xЉ10=0ЃЌ
ећРэЃЌЕУ
ЃЈxЉ5ЃЉЃЈx+2ЃЉ=0ЃЌ
НтЕУy1=5ЃЌy2=Љ2ЃЈЩсШЅЃЉЃЌ
ЙЪa2+b2=5ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌвбжЊЁЯC=90ЁуЃЌЁЯB=55ЁуЃЌЕуDдкБпBCЩЯЃЌBD=2CD.АбЯпЖЮBD ШЦзХЕуDФцЪБеыа§зЊІС(0ЃМІСЃМ180)ЖШКѓЃЌШчЙћЕуBЧЁКУТфдкRtЁїABCЕФБпЩЯЃЌФЧУДІС=__________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCD жаЃЌAB=4ЃЌAD=aЃЌЕуPдкADЩЯЃЌЧвAP=2ЃЌЕуEЪЧБпABЩЯЕФЖЏЕуЃЌвдPEЮЊБпзїжБНЧЁЯEPFЃЌЩфЯпPFНЛBCгкЕуFЃЌСЌНгEFЃЌИјГіЯТСаНсТлЃКЂйtanЁЯPFE=![]() ЃЛЂкaЕФзюаЁжЕЮЊ10.дђЯТСаЫЕЗЈе§ШЗЕФЪЧ( )
ЃЛЂкaЕФзюаЁжЕЮЊ10.дђЯТСаЫЕЗЈе§ШЗЕФЪЧ( )
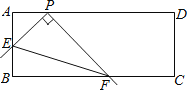
A.ЂйЂкЖМЖдB.ЂйЂкЖМДэC.ЂйЖдЂкДэD.ЂйДэЂкЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцФкгавЛЕШбќRtЁїABCЃЌЁЯACB=90ЁуЃЌЕуAдкжБЯпlЩЯЃЎЙ§ЕуCзїCEЁЭ1гкЕуEЃЌЙ§ЕуBзїBFЁЭlгкЕуFЃЌВтСПЕУCE=3ЃЌBF=2ЃЌдђAFЕФГЄЮЊЃЈЁЁЁЁЃЉ

A. 5 B. 4 C. 8 D. 7
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌОиаЮABCDжаЃЌABЃН8ЃЌADЃН6ЃЛЕуEЪЧЖдНЧЯпBDЩЯвЛЖЏЕуЃЌСЌНгCEЃЌзїEFЁЭCEНЛABБпгкЕуFЃЌвдCEКЭEFЮЊСкБпзїОиаЮCEFGЃЌзїЦфЖдНЧЯпЯрНЛгкЕуHЃЎ

ЃЈ1ЃЉШчЭМ2ЃЌЕБЕуFгыЕуBжиКЯЪБЃЌЧѓCEКЭCGЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌЕБЕуEЪЧBDжаЕуЪБЃЌЧѓCEКЭCGЕФГЄЃЛ
ЃЈ3ЃЉдкЭМ1ЃЌСЌНгBGЃЌЕБОиаЮCEFGЫцзХЕуEЕФдЫЖЏЖјБфЛЏЪБЃЌВТЯыЁїEBGЕФаЮзДЃПВЂМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=5ЃЌBC=7ЃЌEЮЊBCЩЯЕФЖЏЕуЃЌНЋОиаЮбижБЯпAEЗелЃЌЪЙЕуBЕФЖдгІЕуBЃЇТфдкЁЯADCЕФЦНЗжЯпЩЯЃЌЙ§ЕуBЃЇзїBЃЇFЁЭBCгкЕуFЃЌЧѓЁїBЃЇEFЕФжмГЄ______.
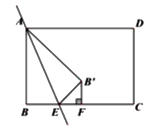
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЕуEЪЧCDЕФжаЕуЃЌНЋЁїBCEбиBEелЕўКѓЕУЕНЁїBEFЁЂЧвЕуFдкОиаЮABCDЕФФкВПЃЌНЋBFбгГЄНЛADгкЕуGЃЎШє![]() ЃЌдђ
ЃЌдђ![]() =__ЃЎ
=__ЃЎ
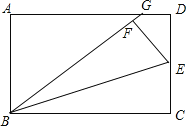
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЬсЩ§бЇЩњЕФвеЪѕЫибјЃЌФГаЃМЦЛЎПЊЩшЫФУХбЁаоПЮГЬЃКЩљРжЁЂЮшЕИЁЂЪщЗЈЁЂЩугАЃЎвЊЧѓУПУћбЇЩњБиаыбЁаоЧвжЛФмбЁаовЛУХПЮГЬЃЌЮЊБЃжЄМЦЛЎЕФгааЇЪЕЪЉЃЌбЇаЃЫцЛњЖдВПЗжбЇЩњНјааСЫвЛДЮЕїВщЃЌВЂНЋЕїЫНсЙћЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦБэКЭЭГМЦЭМЃЎ
бЇЩњбЁаоПЮГЬЭГМЦБэ
ПЮГЬ | ШЫЪ§ | ЫљеМАйЗжБШ |
ЩљРж | 14 |
|
ЮшЕИ | 8 |
|
ЪщЗЈ | 16 |
|
ЩугА |
|
|
КЯМЦ |
|
|

ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() ЁЁЁЁЃЌ
ЁЁЁЁЃЌ![]() ЁЁЁЁЃЎ
ЁЁЁЁЃЎ
ЃЈ2ЃЉЧѓГі![]() ЕФжЕВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЕФжЕВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ3ЃЉИУаЃга1500УћбЇЩњЃЌЧыФуЙРМЦбЁаоЁАЩљРжЁБПЮГЬЕФбЇЩњгаЖрЩйУћЃЎ
ЃЈ4ЃЉЦпЃЈ1ЃЉАрКЭЦпЃЈ2ЃЉАрИїга2ШЫбЁаоЁАЮшЕИЁБПЮГЬЧвгаЮшЕИЛљДЁЃЌбЇаЃзМБИДгет4ШЫжаЫцЛњГщШЁ2ШЫБрХХЁАЮшЕИЁБдкПЊАрвЧЪНЩЯБэбнЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЧѓЫљГщШЁЕФ2ШЫЧЁКУРДздЭЌвЛИіАрМЖЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
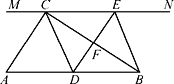
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЙ§ЕуCЕФжБЯпMNЁЮABЃЌDЮЊABБпЩЯвЛЕуЃЌЙ§ЕуDзїDEЁЭBCЃЌНЛжБЯпMNгкEЃЌДЙзуЮЊFЃЌСЌНгCDЃЌBE.
ЃЈ1ЃЉЧѓжЄЃКCEЃНADЃЛ
ЃЈ2ЃЉЕБDЮЊABжаЕуЪБЃЌЫФБпаЮBECDЪЧЪВУДЬиЪтЫФБпаЮЃПЫЕУїФуЕФРэгЩЃЛ
ЃЈ3ЃЉШєDЮЊABжаЕуЃЌдђЕБЁЯAЕФДѓаЁТњзуЪВУДЬѕМўЪБЃЌЫФБпаЮBECDЪЧе§ЗНаЮЃПЧыЫЕУїФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com