
【题目】如图,Rt△BOA与Rt△COA的斜边在x轴上,BA=6,A(10,0),AC与OB相交于点E,且CA=CO,连接BC,下列判断一定正确的是( )
①△ABE∽△OCE;②C(5,5);③BC=![]() ;④S△ABC=3.
;④S△ABC=3.

A. ①③ B. ②④ C. ①②③ D. ①②③④
【答案】D
【解析】
如图,作CF⊥OA于F,BH⊥OA于H,连接BF.①正确,根据两角对应相等两三角形相似即可判断;①正确,利用等腰直角三角形想的性质即可判断;③正确,求出点B坐标,利用两点间距离公式计算即可;④正确,利用分割法计算即可;
如图,作CF⊥OA于F,BH⊥OA于H,连接BF.
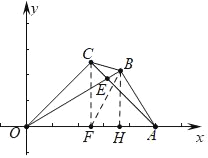
∵∠OCE=∠ABE=90°,∠OEC=∠AEB,
∴△ABE∽△OCE,故①正确,
∵A(10,0),
∴OA=10,
∵OC=CA,∠OCA=90°,CF⊥OA,
∴OF=AF=CF=5,
∴C(5,5),故②正确,
在Rt△ABO中,∵OB=![]() =8,
=8,
∵![]() OABH=
OABH=![]() OBAB,
OBAB,
∴BH=![]() ,
,
∵tan∠BOH=![]() ,
,
∴![]() ,
,
∴OH=![]() ,
,
∴B(![]() ,
,![]() ),
),
∵C(5,5),
∴BC=![]() ,故③正确,
,故③正确,
S△ABC=S△CFB+S△AFB﹣S△ACF=![]() ×5×(
×5×(![]() ﹣5)+
﹣5)+![]() ×5×
×5×![]() ﹣
﹣![]() =3,故④正确,
=3,故④正确,
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
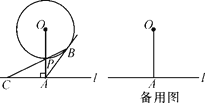
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
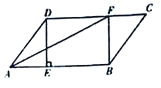
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
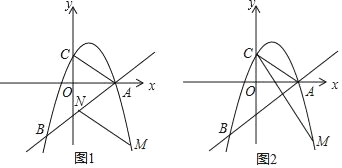
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3与直线y=x﹣3交于点A(3,0)和点B(﹣2,n),与y轴交于点C.
(1)求出抛物线的函数表达式;
(2)在图1中,平移线段AC,点A、C的对应点分别为M、N,当N点落在线段AB上时,M点也恰好在抛物线上,求此时点M的坐标;
(3)如图2,在(2)的条件下,在抛物线上是否存在点P(不与点A重合),使△PMC的面积与△AMC的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
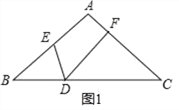
【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,求证:DECD=DFBE
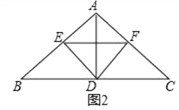
(2)D为BC中点如图2,连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
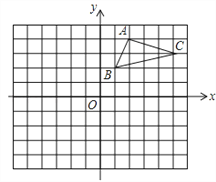
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标A1 ________________.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标A2__________________.
(3) △ABC是否为直角三角形?答_________(填是或者不是).
(4)利用格点图,画出BC边上的高AD,并求出AD的长,AD=_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com