
【题目】定义:四条边都相等且四个角都是直角的四边形叫做正方形。我校“快乐走班”数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
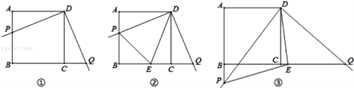
(1)求证:DP=DQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
【答案】 (1)证明见解析;(2)猜测:PE=QE.证明见解析; (3)S△DEP =![]() .
.
【解析】试题分析:本题是一道几何证明题,主要考查了正方形的性质、全等三角形的性质与判定、勾股定理等知识点,试题难度不大,但要注意第(3)题中认真计算,避免出错.
求证DP=DQ;只需证明△ADP≌△CDQ即可得到DP=DQ.解题的关键是找出∠PDC的两个余角相等即∠ADP =∠CDQ,两三角形全等的条件就具备了.
PE=QE.只需证明△PDE≌△QDE即可得到,由(1)的结论DP=DQ加上DE是∠PDQ的平分线易用SAS证得结论.
(3)由AB:AP=3:4,AB=6可求AP=8,BP=2;直接由(1)和(2)的结论AP=CQ、PE=QE设CE=x,则PE=8-x,利用勾股定理求得Rt△PEB的边PE,由此可得EQ的长度,这样△DEP的面积就不难求得了.
试题解析:
(1)证明:∵四边形ABCD是正方形
∴DA=DC,∠DAP=∠DCQ=90°
∵∠PDQ=90°
∴∠ADP+∠PDC=90°
∠CDQ+∠PDC=90°
∠ADP=∠CDQ
在△ADP与△CDQ中
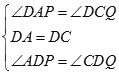
∴△ADP≌△CDQ(ASA)
∴DP=DQ
(2)解:PE=QE.证明如下:
∵ DE是∠PDQ的平分线
∴∠PDE=∠QDE
在△PDE与△QDE中
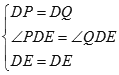
∴△PDE≌△QDE(SAS)
∴PE=QE
(3)解:∵AB:AP=3:4,AB=6
∴AP=8,BP=2,
由(1)知:△ADP≌△CDQ 则AP=CQ=8
由(2)知:△PDE≌△QDE,PE=QE
设CE=x,则PE=QE=CQ-CE=8-x
在Rt△PEB中,BP=2,BE=6+x,PE=8-x
由勾股定理得:22+(6+x)2=(8-x)2
解得:x=![]()
∴![]()
![]()
∴△DEP的面积为:![]()
![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(满分100分)
分数段/分 | 61~70 | 71~80 | 81~90 | 91~100 |
人数/人 | 2 | 8 | 6 | 4 |
若已知成绩在91-100分的同学为优胜者.那么优胜率为%。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y﹣3与3x+1成正比例,且x=2时,y=6.5.
(1)求y与x之间的函数关系式,并指出它是什么函数;
(2)若点(a,2)在这个函数的图象上,求a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.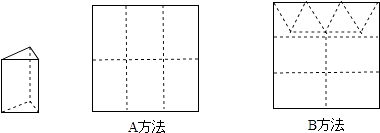
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
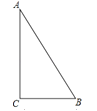
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
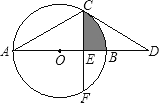
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
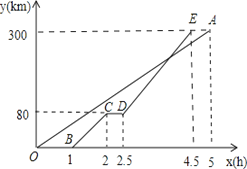
(1)在CD段轿车停留了________小时;
(2)求线段DE对应的函数关系式;
(3)当轿车出发几小时后两车相距30km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90![]() ,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED=
,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED= ![]() ;②
;②![]() ;③∠ADF=
;③∠ADF= ![]() ;④CE=DF.正确的是( )
;④CE=DF.正确的是( )
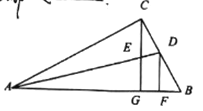
A. ①②④ B. ②③④ C. ①③ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com