
����Ŀ������֪��|x|�ļ�������������������x��Ӧ�ĵ���ԭ��ľ��룬��|x|=|x��0|��Ҳ����˵|x|��ʾ����������x����0��Ӧ��֮��ľ��룻������ۿ����ƹ�Ϊ��|x��y|��ʾ����������x��y��Ӧ��֮��ľ��룻�ڽ����У����dz������þ���ֵ�ļ������壮
�ٽⷽ��|x|=2��������������������ԭ�����Ϊ2�ĵ��Ӧ����Ϊ��2�����÷��̵Ľ�Ϊx=��2��
���ڷ���|x��1|=2�У�x��ֵ���������ϵ�1�ľ���Ϊ2�ĵ��Ӧ��������Ȼx=3��x=��1��
���ڷ���|x��1|+|x+2|=5�У���Ȼ�÷��̱�ʾ��������1�ͩ�2�ľ���֮��Ϊ5 �ĵ��Ӧ��xֵ����������1�ͩ�2�ľ���Ϊ3�����㷽�̵�x�Ķ�Ӧ����1���ұ�2����ߣ���x�Ķ�Ӧ����1���ұߣ���ͼʾ��֪��x=2��ͬ������x�Ķ�Ӧ���ک�2����ߣ��ɵ�x=��3������ԭ���̵Ľ���x=2��x=��3������������Ķ����ϣ�����������⣺
(1)����|x|=5�Ľ���_______________��
��2������|x��2|=3�Ľ���_________________��
��3������ͼʾ���ⷽ��|x��3|+|x+2|=9��

���𰸡���1��x=5��-5 ����2��x=5��-1����3��x=5��-4.
�����������������
��1������|x|=5��ʾ����������x����0��Ӧ��֮��ľ��룬����x=��5��
��2������|x-2|=3�У�x��ֵ���������ϵ�2�ľ���Ϊ3�ĵ��Ӧ��������Ȼx=5��-1��
��3������|x-3|+|x+2|=9��ʾ��������3��-2�ľ���֮��Ϊ9�ĵ��Ӧ��xֵ����������3��-2�ľ���Ϊ5�����㷽�̵�x�Ķ�Ӧ����3���ұ�-2����ߣ���ͼ���ɽ��
�����������1��������������ԭ�����Ϊ5�ĵ��Ӧ����Ϊ��5��
���|x|=5�Ľ�Ϊx=��5��
��2�����ڷ���|x-2|=3�У�x��ֵ�������ϵ�2�ľ���Ϊ3�ĵ��Ӧ������
���|x-2|=3�Ľ���x=5��-1��
![]()
��3������������3��-2�ľ���Ϊ5��5��9��
�����㷽��|x-3|+|x+2|=9��x�Ķ�Ӧ����3���ұ�-2����ߣ�
![]()
��x�Ķ�Ӧ����3���ұߣ���ͼʾ��֪��x=5��
��x�Ķ�Ӧ����-2����ߣ���ͼʾ��֪��x=-4��
����ԭ���̵Ľ���x=5��x=-4��


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
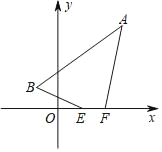
����Ŀ����֪��A��3��4������B����1��1������x������������E��F����EF=1���߶�EF��x����ƽ�ƣ����ı���ABEF���ܳ�ȡ����Сֵʱ����E������Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
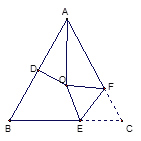
����Ŀ����ͼ�� ![]() �У�
�У� ![]() ,
,![]() ,
, ![]() ��ƽ������
��ƽ������![]() �Ĵ�ֱƽ���߽��ڵ�
�Ĵ�ֱƽ���߽��ڵ�![]() ,��
,��![]() ��
��![]() (
(![]() ��
��![]() ��,
��, ![]() ��
��![]() ��)�۵�����
��)�۵�����![]() ���
���![]() ǡ���غϣ���
ǡ���غϣ���![]() �Ķ����ǣ� ��
�Ķ����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˿�չ���������˶�����ѧ��ÿ���ܶ���һСʱ��ijѧУȥ������Ʒ�̵깺����������������ÿֻ����100Ԫ������ÿֻ����50Ԫ��������Ʒ�̵���ѧУ�ṩ�����Żݷ���������һֻ������һֻ����������������۵�80%�����ѧУҪ����������Ʒ�̵깺������30ֻ������xֻ��x>30����
��1������ѧУ�������ٹ��������踶�� Ԫ�������踶�� Ԫ���ú�x��ʽ�ӱ�ʾ����
����ѧУ�������ڹ��������踶�� Ԫ�������踶�� Ԫ���ú�x��ʽ�ӱ�ʾ����
��2����x=40����ͨ������˵���������١����������ַ��������Ϊ���㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪CΪ�߶�AB���е㣬EΪ�߶�AB�ϵĵ㣬��DΪ�߶�AE���е�.
��1�����߶�AB=a��CE=b��|a��15|+��b��4.5��2=0����a��b��ֵ��
��2����ͼ1���ڣ�1���������£����߶�DE�ij���
��3����ͼ2����AB=15��AD=2BE�����߶�CE�ij�.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̨������Ϊ����ȫ��ƶ��ʦ��������һ�վ�������ס�����У��ʦ�����30000Ԫ����֪��������������ѧУ��ʦ��x�ˣ���ɵ÷���![]() �����ݴ��龰������������������ʾ��ȱʧ������Ӧ���� ��
�����ݴ��龰������������������ʾ��ȱʧ������Ӧ���� ��
A. ��У��ʦ�ȼ�У��ʦ�˾����20Ԫ���Ҽ�У��ʦ����������У��ʦ��������20%
B. ��У��ʦ����У��ʦ�˾����20Ԫ������У��ʦ�������ȼ�У��ʦ��������20%
C. ��У��ʦ����У��ʦ�˾����20Ԫ���Ҽ�У��ʦ����������У��ʦ��������20%
D. ��У��ʦ�ȼ�У��ʦ�˾����20Ԫ������У��ʦ�������ȼ�У��ʦ��������20%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������ȥ�̵깺��ͬһƷ�Ƶ�Ӧ���ƺ��ֵ�Ͳ���鿴���ۺ��֣�����һ��Ӧ���ƺ�5���ֵ�Ͳ����50Ԫ������3��Ӧ���ƺ�2���ֵ�Ͳ����85Ԫ��
��1�������Ʒ��Ӧ���ơ��ֵ�Ͳ�Ķ��۷ֱ��Ƕ���Ԫ��
��2������̸���̵����ù�˾����һ����Ʒ��Ӧ��������һ����Ʒ���ֵ�Ͳ���Żݣ�����ù�˾��Ҫ�ֵ�Ͳ�ĸ�����Ӧ���Ƹ�����2������8�����Ҹù�˾����Ӧ���ƺ��ֵ�Ͳ���ܷ��ò�����670Ԫ����ô�ù�˾���ɹ�����ٸ���Ʒ��Ӧ���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���ACB=90�㣬AC=BC=4��MΪAB���е㣮D������BC��һ�����㣬����AD�����߶�AD�Ƶ�A��ʱ����ת90��õ��߶�AE������ED��NΪED���е㣬����AN��MN�� 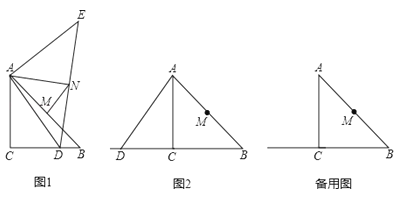
��1����ͼ1����BD=2ʱ��AN���ڶ��٣���NM��AB��λ�ù�ϵ�ǣ�
��2����4��BD��8ʱ��
�������ⲹȫͼ2��
���жϣ�1����NM��AB��λ�ù�ϵ�Ƿ����仯����֤����Ľ��ۣ�
��3������ME���ڵ�D�˶��Ĺ����У���BD�ij�Ϊ��ֵʱ��ME�ij���С����Сֵ�Ƕ��٣���ֱ��д�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com