
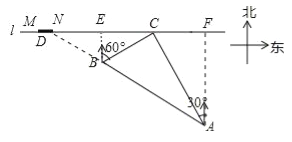
����Ŀ����ͼ����һ����ֱ�Ķ�������l����һ��Ϊ1.5km����ͷMN�͵���C������C����ͷ�Ķ���N��20km.һ�ִ���36km/h���ٶȺ��У�����10��00��A����õ���Cλ���ִ��ı�ƫ��30����������10��40��B����õ���Cλ���ִ��ı�ƫ��60�������������C���12km.
(1)���ִ��մ��ٶ��뺽����ʱ���ﺣ���ߣ�
(2)���ִ����ı亽���ִ��ܷ�ͣ������ͷ����˵������(�ο����ݣ� ![]() ��1.4��
��1.4�� ![]() ��1.7)��
��1.7)��

���𰸡���1��11��00����2���ܣ����ɼ�����.
�������������������1���ӳ�AB��������l�ڵ�D������B��BE��������l�ڵ�E������A��AF��l��F����֤��ABC��ֱ�������Σ���֤����BAC=30���������BD�ij����ɽ�����⣮��2����RT��BEC�У����CD�ij��ȣ���CN��CM�Ƚϼ��ɽ�����⣮
�����������1���ӳ�AB��������l�ڵ�D������B��BE��������l�ڵ�E������A��AF��l��F����ͼ��ʾ��
�ߡ�BEC=��AFC=90������EBC=60������CAF=30����
���ECB=30������ACF=60����
���BCA=90����
��BC=12��AB=36��![]() =24��
=24��
��AB=2BC��
���BAC=30������ABC=60����
�ߡ�ABC=��BDC+��BCD=60����
���BDC=��BCD=30����
��BD=BC=12��
��ʱ��t=![]() =
=![]() Сʱ=20���ӣ�
Сʱ=20���ӣ�
���ִ��մ��ٶ��뺽��������11����00���ﺣ���ߣ�
��2����BD=BC��BE��CD��
��DE=EC��
��RT��BEC����BC=12����BCE=30����
��BE=6��EC=6![]() ��10.2��
��10.2��
��CD=20.4��
��20��20.4��21.5��
���ִ����ı亽���ִ�����ͣ������ͷ��


 �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬D��BC����һ�㣬��DBΪֱ���ġ�O����AB���е�E����AD���ӳ����ڵ�F������EF.
(1)��֤����1����F��
(2)��sinB��![]() ��EF��2
��EF��2![]() ����CD�ij���
����CD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ͼ��滮����6��������ϼɽվ�����Ͼ���վ��ȫ��32100�ף���������ÿ�ѧ��������ʾΪ�� ��
A.321��102
B.32.1��103
C.3.21��104
D.3.21��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ƽ���ʽ���㣬������ǣ� ��
A. (b+a)(a-b)=a2-b2B. (m2+n2)(m2-n2)=m4-n4
C. (2x+1)(2x-1)=2x2-1D. (2-3x)(-3x-2)=9x2-4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ij���д�һ¥����¥��һ�Զ����ݣ�ͼ���Dz���ʾ��ͼ����֪�Զ�����AB���¶�Ϊ1��2.4��AB�ij�����13�ף�MN�Ƕ�¥¥����MN��PQ��C��MN�ϴ����Զ����ݶ���B�����Ϸ���һ�㣬BC��MN�����Զ����ݵ�A�����C�������Ϊ42�������¥�IJ��BCԼΪ(��ȷ��0.1�ף�sin42���0.67��tan42���0.90)(����)

A. 10.8�� B. 8.9�� C. 8.0�� D. 5.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ʵؾ��ȵ�����������ĸ��������α�������-2��0��1��2�������������Σ�����һ������ֱַ���a��b��������ΪM��ĺᡢ�����꣬���M��a��b��������A��-2��0����B��2��0����C��0��2��Ϊ������������ڣ������߽磩�ĸ����ǣ�������
A��![]() B��
B��![]() C��
C��![]() D��
D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A1��A2��x���ϣ���B1��B2��y���ϣ�������ֱ�ΪA1(1��0)��A2(2��0)��B1(0��1)��B2(0��2)���ֱ���A1��A2��B1��B2���е������������OΪ�����������Σ������������ǵ��������εĸ�����(����)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA����1��3����B����1��1����C����3��2��.
��1���뻭����ABC����y��ԳƵġ�A1B1C1��
��2����ԭ��OΪλ�����ģ�����A1B1C1�Ŵ�Ϊԭ����2�����õ���A2B2C2�������A1B1C1���A2B2C2�����.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com