
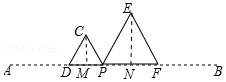
【题目】已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示. 
(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
【答案】
(1)解:∵△CDP和△EFP是等边三角形,
∴CD=PC=PD,EF=EP=PF,AP=3PD,BP=3PF,
∵DF=PD+PF=2,
∴AB=AP+BP=3DF=3×2=6
(2)解:没有最大值,理由如下:
设CD=PC=PD=x,则EF=EP=PF= ![]() (18﹣3x)=6﹣x,
(18﹣3x)=6﹣x,
作CM⊥PD于M,EN⊥PF于N,
则DM= ![]() PD=
PD= ![]() x,PN=
x,PN= ![]() PF=
PF= ![]() (6﹣x),
(6﹣x),
∴CM= ![]() DM=
DM= ![]() x,EN=
x,EN= ![]() (6﹣x),
(6﹣x),
∴△CDP的面积= ![]() PDCM=
PDCM= ![]() x2,△EFP的面积=
x2,△EFP的面积= ![]() (6﹣x)2,
(6﹣x)2,
∴等边△CDP和△EFP的面积之和S= ![]() x2+
x2+ ![]() (6﹣x)2=
(6﹣x)2= ![]() x2﹣3
x2﹣3 ![]() x+9
x+9 ![]() ,
,
∵ ![]() >0,
>0,
∴S有最小值,没有最大值.
【解析】(1)由等边三角形的性质容易得出结果;(2)设CD=PC=PD=x,则EF=EP=PF=6﹣x,求出等边△CDP和△EFP的面积之和S= ![]() x2﹣3
x2﹣3 ![]() x+9
x+9 ![]() ,
, ![]() >0,得出S有最小值,没有最大值.
>0,得出S有最小值,没有最大值.
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a),还要掌握等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】某公司员工分别住在A、B、C三个住宅区,A区有25人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应设在( )
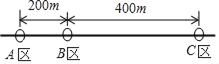
A. A区 B. B区 C. A区或B区 D. C区
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE. 
(1)求证:BC是⊙O的切线;
(2)若tan∠G= ![]() ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某地有一地下工程,其底面是正方形,面积为405m2,四个角是面积为5m2的小正方形渗水坑,根据这些条件如何求a的值?与你的同伴进行交流.
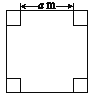
下面是小康提供的解题方案,根据解题方案请你完成本题的解答过程:
①设大正方形的边长为x m,小正方形的边长为y m,那么根据题意可列出关于x的方程为_______,关于y的方程为_______;
②利用平方根的意义,可求得x=________(取正值,结果保留根号),y=________(取正值,结果保留根号);
③所以a=x-2y=____________=__________(结果保留根号);
④答:________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题. 随着人们环保意识的增强及科学技术的进步,各种绿色环保新产品进入千家万户,今年一月份小楠家将天然气热水器换成了太阳能热水器,减少天然气的用量,去年12月份小楠家的天然气费一共是96元,从今年一月份起天然气费价格每立方米上涨了25%,小楠家2月份的用气量比去年12月份少10立方米,2月份的天然气费一共是90元,请你求小楠家今年2月份用气量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与x轴相交于点B(1,0)和点C(9,0)两点,与y轴的负半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴正半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.
(1)求点A坐标和⊙P的半径;
(2)求抛物线的解析式;
(3)当△MOB与以点B、C、D为顶点的三角形相似时,求△CDN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com