
【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
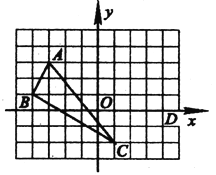
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标:
A′(___________); B′(___________);C′(___________)。
(3)求△ABC的面积。
【答案】(1)作图见解析;(2)A′(0,5); B′(-1,3);C′(4,0);(3)6.5
【解析】(1)根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置,然后顺次连接即可;(2)根据平面直角坐标系写出各点的坐标即可;(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
解:(1)△A′B′C′如图所示;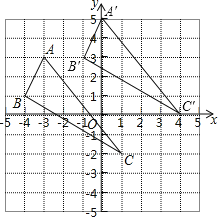
(2)A′(0,5),B′(-1,3),C′(4,0);
(3)△ABC的面积=5×5-![]() ×1×2-
×1×2-![]() ×5×3-
×5×3-![]() ×4×5
×4×5
=25-1-7.5-10
=25-18.5
=6.5.
“点睛”本题考查了利用平移变换作图,三角形的面积,需熟练掌握网格结构,准确找出对应点的位置.


科目:初中数学 来源: 题型:
【题目】2016年春节期间,在网络上搜索“开放二孩”,能搜索到与之相关的结果个数约为45100000,这个数用科学记数法表示为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因市场竞争激烈,国商进行促销活动,决定对学习用品进行打八折出售,打折前,买2本笔记本和1支圆珠笔需要18元,买1本笔记本和2支圆珠笔需要12元.
(1)求打折前1本笔记本,1支圆珠笔各需要多少元.
(2)在促销活动时间内,购买50本笔记本和40支圆珠笔共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(单位:吨)与运输时间x(单位:天)之间有怎样的函数关系式?
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:

已知该公司的加工能力是:粗加工每天加工该种蔬菜的重量是精加工的3倍,但两种加工不能同时进行,受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售.
(1)若要求15天刚好加工完140吨蔬菜,如果绿色蔬菜先精加工20吨,剩下的再进行粗加工,正好按时完成,求精加工和粗加工每天各能加工的吨数.
(2)若要求将140吨蔬菜全部加工完不超过13天,并且两种加工方式都要有,先精加工后粗加工,问怎样分配加工时间(时间取整)利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
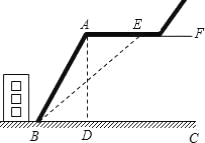
【题目】某中学紧挨一座山坡,如图所示,已知AF∥BC,AB长30米,∠ABC=66°,为防止山体滑坡,需要改造山坡,改造后的山坡BE与地面成45°角,求AE是多少米?(精确到1米)
(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com