
【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
【答案】(1)y=﹣![]() (x﹣2)2
(x﹣2)2
(2)△ABC∽△N1BN2
(3)![]()
(4)![]()
【解析】
试题分析:(1)用待定系数法求,即可;
(2)由对称的特点得出∠N1BN2=2∠DBC结合菱形的性质即可;
(3)先判定出,当BN⊥CD时,BN最短,再利用△ABC∽△N1BN2得到比例式,求解,即可;
(4)先建立PE=![]() m2﹣
m2﹣![]() m+2函数解析式,根据抛物线的特点确定出最小值.
m+2函数解析式,根据抛物线的特点确定出最小值.
试题解析:(1)由已知,设抛物线解析式为y=a(x﹣2)2
把D(0,﹣1)代入,得a=﹣![]()
∴y=﹣![]() (x﹣2)2
(x﹣2)2
(2)如图1,连结BN.
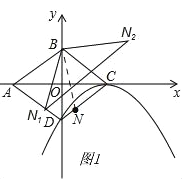
∵N1,N2是N的对称点
∴BN1=BN2=BN,∠N1BD=∠NBD,∠NBC=∠N2BC
∴∠N1BN2=2∠DBC
∵四边形ABCD是菱形
∴AB=BC,∠ABC=2∠DBC
∴∠ABC=∠N1BN2,![]()
∴△ABC∽△N1BN2
(3)∵点N是CD上的动点,
∴点到直线的距离,垂线段最短,
∴当BN⊥CD时,BN最短.
∵C(2,0),D(0,﹣1)
∴CD=![]() ,
,
∴BNmin=![]() ,
,
∴BN1min=BNmin=![]() ,
,
∵△ABC∽△N1BN2
∴![]() ,
,
N1N2min=![]() ,
,
(4)如图2,
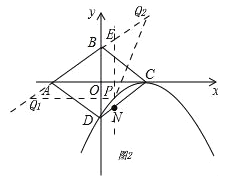
过点P作PE⊥x轴,交AB于点E.
∵∠PQA=∠BAC
∴PQ1∥AC
∵菱形ABCD中,C(2,0),D(0,﹣1)
∴A(﹣2,0),B(0,1)
∴lAB:Y=![]() x+1
x+1
不妨设P(m,﹣![]() (m﹣2)2),则E(m,
(m﹣2)2),则E(m,![]() m+1)
m+1)
∴PE=![]() m2﹣
m2﹣![]() m+2
m+2
∴当m=1时,![]()
此时,PQ1最小,最小值为![]() =
=![]() ,
,
∴PQ1=PQ2=![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,EF∥MN,∠1=115°,

(1)求∠2和∠4的度数;
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳:如果一个角的两边分别平行于另一个角的两边,那么这两个角___________;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的两倍,求这两个角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
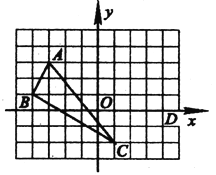
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标:
A′(___________); B′(___________);C′(___________)。
(3)求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中正确的是( )
A. 圆周角的度数等于它所对弧的度数的一半 B. 三点确定一个圆
C. 圆有四条对称轴 D. 各边相等的多边形是正多边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,点A为![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
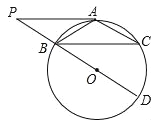
(1)求证:PA是⊙O的切线;
(2)若![]() ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com