
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
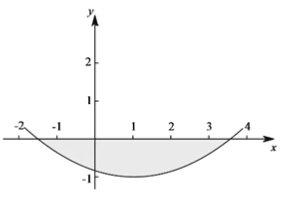
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
【答案】(1)(1,-1);(2)①3;②![]() .
.
【解析】
试题分析:(1)将抛物线表达式变为顶点式,即可得到顶点坐标;
(2)①m=1时,抛物线表达式为![]() ,即可得到A、B的坐标,可得到线段AB上的整点个数;
,即可得到A、B的坐标,可得到线段AB上的整点个数;
②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;令y=0,则![]() ,解方程可得到A、B两点坐标分别为(
,解方程可得到A、B两点坐标分别为(![]() ,0),(
,0),(![]() ,0),即5个整点是以(1,0)为中心向两侧分散,进而得到
,0),即5个整点是以(1,0)为中心向两侧分散,进而得到![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)将抛物线表达式变为顶点式![]() ,则抛物线顶点坐标为(1,-1);
,则抛物线顶点坐标为(1,-1);
(2)①m=1时,抛物线表达式为![]() ,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;
,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;
②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;又有抛物线表达式,令y=0,则![]() ,得到A、B两点坐标分别为(
,得到A、B两点坐标分别为(![]() ,0),(
,0),(![]() ,0),即5个整点是以(1,0)为中心向两侧分散,进而得到
,0),即5个整点是以(1,0)为中心向两侧分散,进而得到![]() ,∴
,∴![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
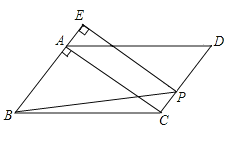
【题目】如图,在平行四边形ABCD中,AB=3,BC=5,对角线AC⊥AB.点P从点D出发,沿折线DC﹣CB以每秒1个单位长度的速度向终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连结BP.设点P的运动时间为t(秒),△BPE的面积为S(平方单位).
(1)AD与BC间的距离是 .
(2)当点P在BC上时,求PE的长(用含t的代数式表示).
(3)求S与t之间的函数关系式.
(4)直接写出PE将平行四边形ABCD的面积分成1:7两部分时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,等边△ABC,点 E 在 BA 的延长线上,点 D 在 BC 上,且 ED=EC.
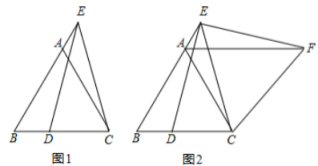
(1)如图 1,求证:AE=DB;
(2)如图 2,将△BCE 绕点 C 顺时针旋转 60°至△ACF(点 B、E 的对应点分别为点 A、F),连接 EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于 AB 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
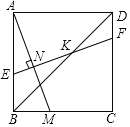
【题目】如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
(1)AE的长为______(用含x的代数式表示);
(2)设EK=2KF,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com